library("SBC")
library("brms")
library("cmdstanr")
library("ggplot2")
library("colorspace")
library("cowplot")
library("future")Intro
Relevant parts of the code given here is inspired by the resources of the great SBC package (Modrák et al., 2023) published at https://hyunjimoon.github.io/SBC/index.html.
Also, coding of posterior p-values is inspired by the split predictive check (Li & Huggins, 2024) R code published at https://github.com/TARPS-group/split-predictive-checks.
Software
We use the statistical software environment R (R Core Team, 2024), and R add-on packages colorspace (Stauffer et al., 2009), SBC (Modrák et al., 2023), brms (Bürkner, 2017, 2018, 2021), cmdstanr (Gabry et al., 2024), ggplot2 (Wickham, 2016), and future (Bengtsson, 2021).
This document is produced using Quarto (Allaire et al., 2024).
Organize R Session
Load packages:
Settings:
rm(list = ls())
options(brms.backend = "cmdstanr")
# Using parallel processing
plan(multisession)
options(SBC.min_chunk_size = 5)
# Setup caching of results
cache_dir <- "./_SBC_cache"
if(!dir.exists(cache_dir)) {
dir.create(cache_dir)
}Data preparation function for graphical uniformity checks:
## from https://github.com/TeemuSailynoja/simultaneous-confidence-bands/tree/main
dat_ecdf_diff <- function (x, variables = NULL, K = NULL,
gamma = NULL, prob = 0.95,
combine_variables = NULL,
ecdf_alpha = NULL, ...,
parameters = NULL) {
if (!is.null(parameters)) {
warning("The `parameters` argument is deprecated use `variables` instead.")
if (is.null(variables)) {
variables <- parameters
}
}
ecdf_data <- data_for_ecdf_plots(x, variables = variables,
prob = prob, K = K, gamma = gamma, combine_variables = combine_variables,
ecdf_alpha = ecdf_alpha, ...)
if (ecdf_data$N < 50 && is.null(K)) {
message("With less than 50 simulations, we recommend using plot_ecdf as it has better fidelity.\n",
"Disable this message by explicitly setting the K parameter. ",
"You can use the strings \"max\" (high fidelity) or \"min\" (nicer plot) or choose a specific integer.")
}
N <- ecdf_data$N
K <- ecdf_data$K
z <- ecdf_data$z
ecdf_df <- dplyr::mutate(ecdf_data$ecdf_df, z_diff = ecdf -
z, type = "sample ECDF")
limits_df_trans <- dplyr::mutate(ecdf_data$limits_df, ymax = upper -
uniform_val, ymin = lower - uniform_val, type = "theoretical CDF")
return(list('ecdf_df' = ecdf_df,
'limits_df_trans' = limits_df_trans))
}Data Generator
The data can be generated using the following code – note that we need to be careful to match the parameter names as brms uses them.
f_generate_y <- function(sim_df,
b_Intercept,
b_x,
grouping_term, ## sd_g__Intercept or r_g
sigma) {
if (is.matrix(grouping_term)) {
r_g <- grouping_term
} else {
G <- length(levels(sim_df$g))
r_g <- matrix(rnorm(n = G, mean = 0, sd = grouping_term),
nrow = G, ncol = 1,
dimnames = list(levels(sim_df$g), "Intercept"))
}
sim_df$'mu' <- exp(b_Intercept +
sim_df$'x' * b_x +
r_g[sim_df$'g'])
sim_df$'sigma' <- sigma
sim_df$'y' <- rnorm(n = nrow(sim_df),
mean = sim_df$'mu',
sd = sim_df$'sigma')
return(sim_df)
}
f_generate_one_sim <- function(N, G) {
prior_mu <- list('b_Intercept' = 0,
'b_x' = 1,
'sd_g__Intercept' = .5,
'sigma' = 1)
prior_sd <- list('b_Intercept' = .1,
'b_x' = .1,
'sd_g__Intercept' = .1,
'sigma' = .1)
b_Intercept <- rnorm(n = 1,
mean = prior_mu$b_Intercept,
sd = prior_sd$b_Intercept)
b_x <- rnorm(n = 1,
mean = prior_mu$b_x,
sd = prior_sd$b_x)
sd_g__Intercept <- rnorm(n = 1,
mean = prior_mu$sd_g__Intercept,
sd = prior_sd$sd_g__Intercept)
sd_g__Intercept <- abs(sd_g__Intercept)
sigma <- rnorm(n = 1,
mean = prior_mu$sigma,
sd = prior_sd$sigma)
sigma <- abs(sigma)
indx <- rep(c(5, 25, 45), c(6, 8, 6))
if (sum(indx) != 500) {
stop("'N' must be 500 currently!")
}
g <- paste0("Group ", formatC(1:G, width = 2, flag = "0"))
g <- sample(g)
g <- rep(g, indx)
g <- as.factor(g)
r_g <- matrix(rnorm(n = G, mean = 0, sd = sd_g__Intercept),
nrow = G, ncol = 1,
dimnames = list(levels(g), "Intercept"))
sim_df_skeleton <- data.frame('x' = 2 * runif(N),
'g' = g)
return(list('variables' = list('b_Intercept' = b_Intercept,
'b_x' = b_x,
'sd_g__Intercept' = sd_g__Intercept,
'r_g' = r_g,
'sigma' = sigma),
'generated' = f_generate_y(sim_df = sim_df_skeleton,
b_Intercept,
b_x,
grouping_term = r_g,
sigma)))
}
f_generate_n_sims <- SBC_generator_function(f_generate_one_sim,
N = 500,
G = 20)
set.seed(0)
datasets <- generate_datasets(f_generate_n_sims, 100)
head(datasets$generated[[1]]) x g mu sigma y
1 0.6933670 Group 11 2.010588 1.127243 1.257388
2 0.6675499 Group 11 1.960995 1.127243 3.026448
3 0.9527025 Group 11 2.583906 1.127243 3.072794
4 1.7843967 Group 11 5.776880 1.127243 6.909938
5 1.7286789 Group 11 5.473749 1.127243 5.033990
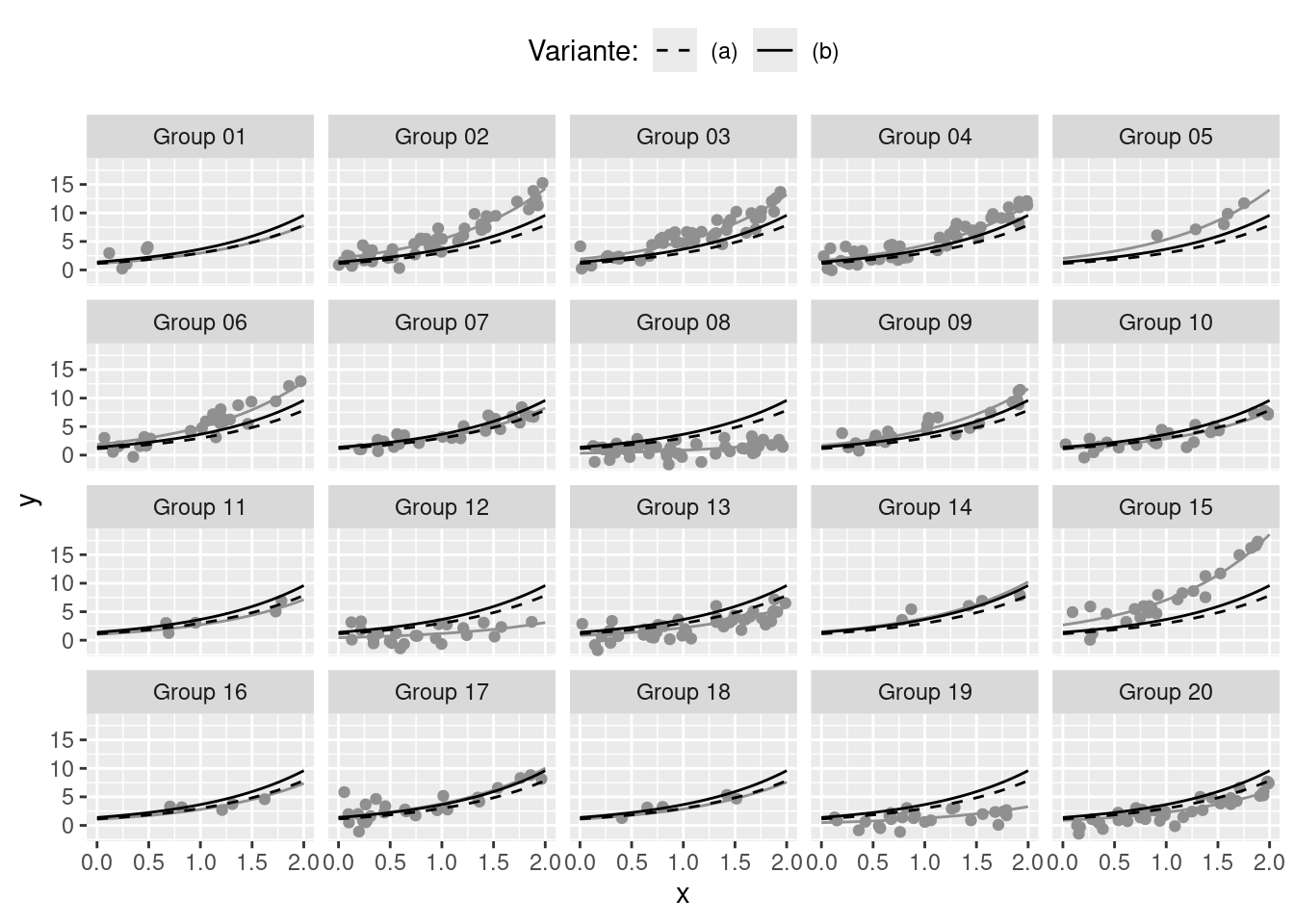
6 0.7799791 Group 14 3.143628 1.127243 3.567889Descriptive Plot
r <- 1
dat <- as.data.frame(expand.grid(x = seq(0, 2, by = .05), g = 1:20))
b <- as.numeric(datasets$variables[r, ])
dat$y <- exp(b[1] + dat$x * b[2] + b[dat$g + 3])
dat$g <- paste0("Group ", formatC(dat$g, width = 2, flag = "0"))
dat$k <- dat$l <- "Single group"
dat <- rbind(dat,
data.frame(x = seq(0, 2, by = .05),
y = exp(b[1] + dat$x * b[2]),
g = "Group 21",
k = "(a)",
l = "Average"),
data.frame(x = seq(0, 2, by = .05),
y = exp(b[1] + dat$x * b[2] + .5 * b[3]^2),
g = "Group 22",
k = "(b)",
l = "Average"))
sdat <- subset(dat, l == "Average")
sdat$g <- NULL
paint <- colorspace::sequential_hcl(n = 20, pal = "Grays")[10]
ggplot(data = datasets$generated[[r]], aes(x = x, y = y)) +
geom_line(data = subset(dat, l != "Average"), color = paint) +
geom_point(, color = paint) +
geom_line(data = sdat, aes(group = k, linetype = k), color = 1) +
scale_linetype_manual(values = c(2, 1)) +
facet_wrap(~ g) +
labs(linetype = "Variante:") +
theme(legend.position = "top")
Backend
priors <-
prior(normal(0,.1), class = "b", coef = "Intercept") +
prior(normal(1,.1), class = "b", coef = "x") +
prior(normal(.5,.1), class = "sd") +
prior(normal(1,.1), class = "sigma")
stan_file_filename <- "brms_log_link_linear_mixed_model.stan"
f_backend <- SBC_backend_brms(bf(y ~ 0 + Intercept + x + (1 | g)),
family = gaussian(link = "log"),
prior = priors,
chains = 1,
template_data = datasets$generated[[1]],
out_stan_file = file.path(cache_dir,
stan_file_filename))
log_lik_log_link_lmm <- derived_quantities(
log_lik = sum(dnorm(y,
mean = exp(b_Intercept + x * b_x + r_g[g]),
sd = sigma,
log = TRUE)))
results <- compute_SBC(datasets,
f_backend,
dquants = log_lik_log_link_lmm,
cache_mode = "results",
cache_location = file.path(cache_dir,
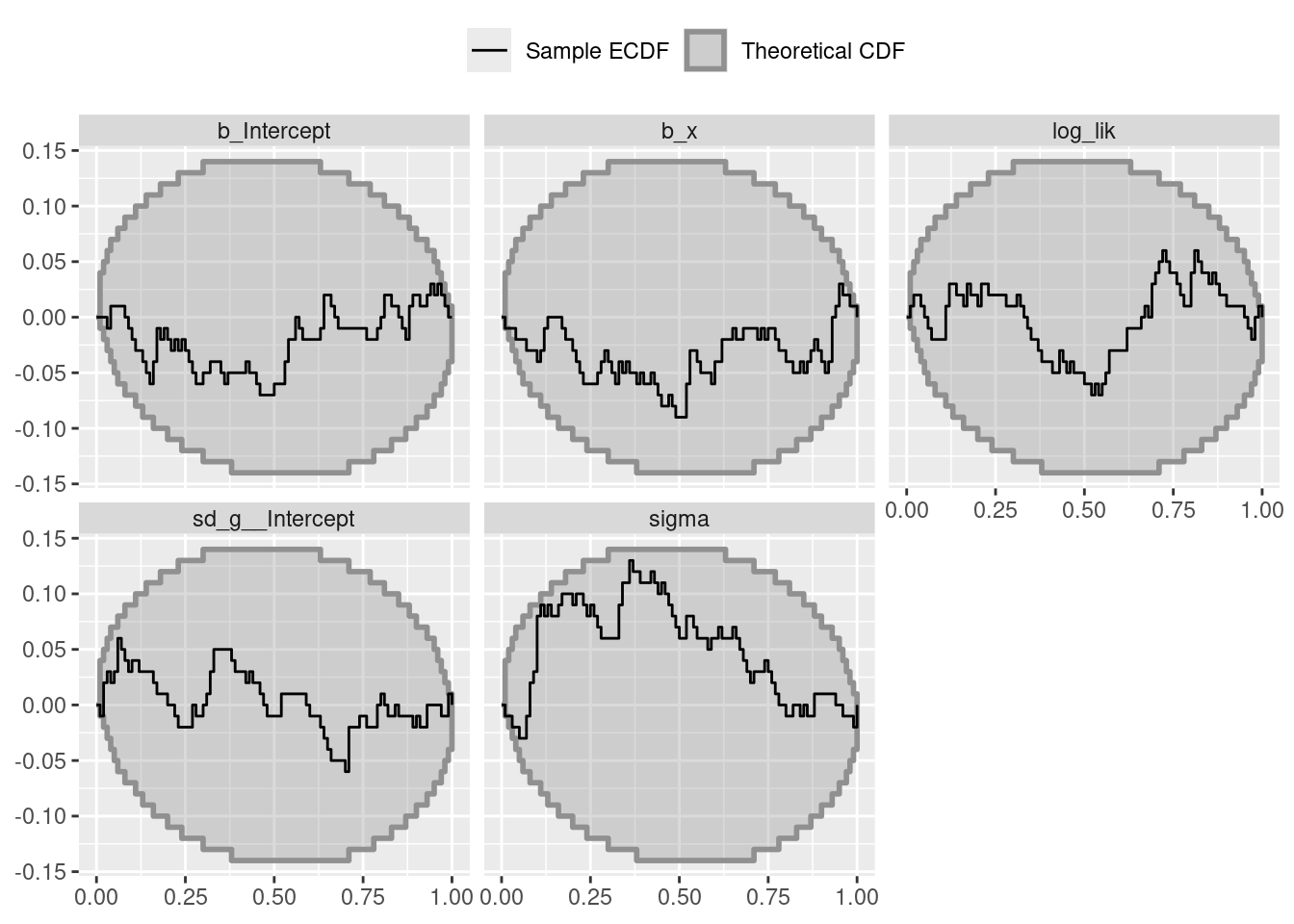
"results_log_link_linear_mixed_model"))tmp <- results$result$stats[, c("sim_id", "variable", "rank")]
tmp <- dat_ecdf_diff(tmp,
variables = c("b_Intercept", "b_x", "sd_g__Intercept", "sigma",
"log_lik"),
max_rank = 99)
tmp$variable <- factor(tmp$variable,
levels = c("b_Intercept", "b_x", "sd_g__Intercept", "sigma",
"log_lik"))
col_color <- c(colorspace::sequential_hcl(n = 20, pal = "Grays")[10], "black")
col_fill <- c(colorspace::sequential_hcl(n = 20, pal = "Grays")[10], "black")
names(col_color) <- names(col_fill) <-
c("theoretical CDF", "sample ECDF")
l <- c('theoretical CDF' = expression("Theoretical CDF"),
'sample ECDF' = expression("Sample ECDF"))ggplot(tmp$ecdf_df, aes(color = type, fill = type)) +
geom_ribbon(data = tmp$limits_df_trans,
aes(x = x, ymax = ymax, ymin = ymin), alpha = .33,
linewidth = 1) +
geom_step(aes(x = z, y = z_diff, group = variable)) +
scale_color_manual(name = "", values = col_color, labels = l) +
scale_fill_manual(name = "", values = col_fill, labels = l) +
scale_alpha_identity() +
xlab(NULL) +
ylab(NULL) +
facet_wrap(~ variable) +
theme(strip.text = element_text(margin = margin(b = 2, t = 2))) +
theme(legend.position = "top")
Calculate QOI-Check
Preparations:
f_predict_brms_gaussian <- function(fit, nd) {
predict(fit, newdata = nd,
summary = F,
allow_new_levels = T,
sample_new_levels = "gaussian")
}
f_predict_brms_uncrtnty <- function(fit, nd) {
predict(fit, newdata = nd,
summary = F,
allow_new_levels = T,
sample_new_levels = "uncertainty")
}
set.seed(123456789)
p_stat_mean_ref_gr_gaussian_a <- p_stat_mean_ref_gr_uncrtnty_a <-
p_stat_mean_ref_gr_gaussian_b <- p_stat_mean_ref_gr_uncrtnty_b <-
p_stat_mean_sim_df_gaussian_a <- p_stat_mean_sim_df_uncrtnty_a <-
p_stat_mean_sim_df_gaussian_b <- p_stat_mean_sim_df_uncrtnty_b <-
## [October 22, 2024]
p_stat_mean_ref_gr_gaussian_c <- p_stat_mean_ref_gr_uncrtnty_c <-
p_stat_mean_ref_gr_gaussian_d <- p_stat_mean_ref_gr_uncrtnty_d <-
p_stat_mean_sim_df_gaussian_c <- p_stat_mean_sim_df_uncrtnty_c <-
p_stat_mean_sim_df_gaussian_d <- p_stat_mean_sim_df_uncrtnty_d <-
##
p_stat_mean_ref_gr_gaussian_e <- p_stat_mean_ref_gr_uncrtnty_e <-
p_stat_mean_ref_gr_gaussian_f <- p_stat_mean_ref_gr_uncrtnty_f <-
p_stat_mean_sim_df_gaussian_e <- p_stat_mean_sim_df_uncrtnty_e <-
p_stat_mean_sim_df_gaussian_f <- p_stat_mean_sim_df_uncrtnty_f <-
##
p_stat_mean_eq_a_a <- p_stat_mean_eq_a_b <- p_stat_mean_eq_a_c <-
p_stat_mean_eq_a_d <- p_stat_mean_eq_a_e <- p_stat_mean_eq_a_f <-
##
p_stat_mean_eq_b_a <- p_stat_mean_eq_b_b <- p_stat_mean_eq_b_c <-
p_stat_mean_eq_b_d <- p_stat_mean_eq_b_e <- p_stat_mean_eq_b_f <-
##
rep(NA, length(results$fits))Loop through the simulation runs and calculate all QOI variants for each run:
for (r in 1:length(results$fits)) {
## Prior in repetition r:
prior_r <- subset(results$stats, sim_id == r)
## Methods a and b:
equation_a <- exp(subset(prior_r, variable == "b_Intercept")$simulated_value +
1 * subset(prior_r, variable == "b_x")$simulated_value)
equation_b <- exp(subset(prior_r, variable == "b_Intercept")$simulated_value +
1 * subset(prior_r, variable == "b_x")$simulated_value +
.5 * (subset(prior_r,
variable == "sd_g__Intercept")$simulated_value^2))
## Reference grid data 'ref_gr':
g <- paste0("g", formatC(101:300, width = 3, flag = "0"))
ref_gr <- data.frame('x' = 1,
'g' = as.factor(g))
## Duplicate observation data 'sim_df':
sim_df <- results$fits[[r]]$data[, c('x', 'g')]
sim_df$x <- 1 ## November 15, 2024
g <- 100 + as.numeric(sim_df$g) ## 'break' original levels
g <- paste0("g", formatC(g, width = 3, flag = "0"))
sim_df$g <- as.factor(g)
## Prior predictions (methods c and d):
y_prior_pred <- f_generate_y(sim_df = ref_gr,
b_Intercept = subset(prior_r,
variable == "b_Intercept")$simulated_value,
b_x = subset(prior_r,
variable == "b_x")$simulated_value,
grouping_term = subset(prior_r,
variable == "sd_g__Intercept")$simulated_value,
sigma = subset(prior_r,
variable == "sigma")$simulated_value)
ref_gr$y_prior_pred <- y_prior_pred$y
rm(y_prior_pred)
y_prior_pred <- f_generate_y(sim_df = sim_df,
b_Intercept = subset(prior_r,
variable == "b_Intercept")$simulated_value,
b_x = subset(prior_r,
variable == "b_x")$simulated_value,
grouping_term = subset(prior_r,
variable == "sd_g__Intercept")$simulated_value,
sigma = subset(prior_r,
variable == "sigma")$simulated_value)
sim_df$y_prior_pred <- y_prior_pred$y
rm(y_prior_pred)
reference_c <- mean(ref_gr$y_prior_pred)
reference_d <- mean(sim_df$y_prior_pred)
b <- datasets$variables[r, ]
b <- as.numeric(b)
## Prior 'uncertainty' for ref_gr:
gamma <- sample(b[grep(x = colnames(datasets$variables),
pattern = "r_g[Group", fixed = T)],
size = 200, replace = T)
gamma <- matrix(gamma, nrow = 200, ncol = 1,
dimnames = list(levels(ref_gr$g), "Intercept"))
ref_gr$y_prior_pred_uncrtnty <- f_generate_y(sim_df = ref_gr,
b_Intercept =
b[which(colnames(datasets$variables) == "b_Intercept")],
b_x =
b[which(colnames(datasets$variables) == "b_x")],
grouping_term = gamma,
sigma =
b[which(colnames(datasets$variables) == "sigma")])$y
## Prior 'uncertainty' for sim_df:
gamma <- sample(b[grep(x = colnames(datasets$variables),
pattern = "r_g[Group", fixed = T)],
size = 20, replace = T)
gamma <- matrix(gamma, nrow = 20, ncol = 1,
dimnames = list(levels(sim_df$g), "Intercept"))
sim_df$y_prior_pred_uncrtnty <- f_generate_y(sim_df = sim_df,
b_Intercept =
b[which(colnames(datasets$variables) == "b_Intercept")],
b_x =
b[which(colnames(datasets$variables) == "b_x")],
grouping_term = gamma,
sigma =
b[which(colnames(datasets$variables) == "sigma")])$y
reference_e <- mean(ref_gr$y_prior_pred_uncrtnty)
reference_f <- mean(sim_df$y_prior_pred_uncrtnty)
B <- as.matrix(results$fits[[r]]) ## Posterior sample
posterior_equation_a <- exp(B[, "b_Intercept"] + 1 * B[, "b_x"])
posterior_equation_b <- exp(B[, "b_Intercept"] + 1 * B[, "b_x"] +
.5 * B[, "sd_g__Intercept"]^2)
Y_rep_ref_gr_g <- f_predict_brms_gaussian(results$fits[[r]], ref_gr)
Y_rep_ref_gr_u <- f_predict_brms_uncrtnty(results$fits[[r]], ref_gr)
Y_rep_sim_df_g <- f_predict_brms_gaussian(results$fits[[r]], sim_df)
Y_rep_sim_df_u <- f_predict_brms_uncrtnty(results$fits[[r]], sim_df)
stat_mean_ref_gr_uncrtnty_a <- stat_mean_ref_gr_gaussian_a <-
stat_mean_ref_gr_uncrtnty_b <- stat_mean_ref_gr_gaussian_b <-
stat_mean_sim_df_uncrtnty_a <- stat_mean_sim_df_gaussian_a <-
stat_mean_sim_df_uncrtnty_b <- stat_mean_sim_df_gaussian_b <-
##
stat_mean_ref_gr_uncrtnty_c <- stat_mean_ref_gr_gaussian_c <-
stat_mean_ref_gr_uncrtnty_d <- stat_mean_ref_gr_gaussian_d <-
stat_mean_sim_df_uncrtnty_c <- stat_mean_sim_df_gaussian_c <-
stat_mean_sim_df_uncrtnty_d <- stat_mean_sim_df_gaussian_d <-
##
stat_mean_ref_gr_uncrtnty_e <- stat_mean_ref_gr_gaussian_e <-
stat_mean_ref_gr_uncrtnty_f <- stat_mean_ref_gr_gaussian_f <-
stat_mean_sim_df_uncrtnty_e <- stat_mean_sim_df_gaussian_e <-
stat_mean_sim_df_uncrtnty_f <- stat_mean_sim_df_gaussian_f <-
##
eq_a_a <- eq_a_b <- eq_a_c <- eq_a_d <- eq_a_e <- eq_a_f <-
eq_b_a <- eq_b_b <- eq_b_c <- eq_b_d <- eq_b_e <- eq_b_f <-
rep(NA, nrow(Y_rep_ref_gr_g))
for (s in 1:nrow(Y_rep_ref_gr_g)) {
ref_gr$y_rep_gaussian <- Y_rep_ref_gr_g[s, ]
ref_gr$y_rep_uncrtnty <- Y_rep_ref_gr_u[s, ]
sim_df$y_rep_gaussian <- Y_rep_sim_df_g[s, ]
sim_df$y_rep_uncrtnty <- Y_rep_sim_df_u[s, ]
## Calculate stats:
stat_mean_ref_gr_gaussian_a[s] <- equation_a < mean(ref_gr$y_rep_gaussian)
stat_mean_ref_gr_uncrtnty_a[s] <- equation_a < mean(ref_gr$y_rep_uncrtnty)
stat_mean_ref_gr_gaussian_b[s] <- equation_b < mean(ref_gr$y_rep_gaussian)
stat_mean_ref_gr_uncrtnty_b[s] <- equation_b < mean(ref_gr$y_rep_uncrtnty)
stat_mean_sim_df_gaussian_a[s] <- equation_a < mean(sim_df$y_rep_gaussian)
stat_mean_sim_df_uncrtnty_a[s] <- equation_a < mean(sim_df$y_rep_uncrtnty)
stat_mean_sim_df_gaussian_b[s] <- equation_b < mean(sim_df$y_rep_gaussian)
stat_mean_sim_df_uncrtnty_b[s] <- equation_b < mean(sim_df$y_rep_uncrtnty)
##
stat_mean_ref_gr_gaussian_c[s] <- reference_c < mean(ref_gr$y_rep_gaussian)
stat_mean_ref_gr_uncrtnty_c[s] <- reference_c < mean(ref_gr$y_rep_uncrtnty)
stat_mean_ref_gr_gaussian_d[s] <- reference_d < mean(ref_gr$y_rep_gaussian)
stat_mean_ref_gr_uncrtnty_d[s] <- reference_d < mean(ref_gr$y_rep_uncrtnty)
stat_mean_sim_df_gaussian_c[s] <- reference_c < mean(sim_df$y_rep_gaussian)
stat_mean_sim_df_uncrtnty_c[s] <- reference_c < mean(sim_df$y_rep_uncrtnty)
stat_mean_sim_df_gaussian_d[s] <- reference_d < mean(sim_df$y_rep_gaussian)
stat_mean_sim_df_uncrtnty_d[s] <- reference_d < mean(sim_df$y_rep_uncrtnty)
##
stat_mean_ref_gr_gaussian_e[s] <- reference_e < mean(ref_gr$y_rep_gaussian)
stat_mean_ref_gr_uncrtnty_e[s] <- reference_e < mean(ref_gr$y_rep_uncrtnty)
stat_mean_ref_gr_gaussian_f[s] <- reference_f < mean(ref_gr$y_rep_gaussian)
stat_mean_ref_gr_uncrtnty_f[s] <- reference_f < mean(ref_gr$y_rep_uncrtnty)
stat_mean_sim_df_gaussian_e[s] <- reference_e < mean(sim_df$y_rep_gaussian)
stat_mean_sim_df_uncrtnty_e[s] <- reference_e < mean(sim_df$y_rep_uncrtnty)
stat_mean_sim_df_gaussian_f[s] <- reference_f < mean(sim_df$y_rep_gaussian)
stat_mean_sim_df_uncrtnty_f[s] <- reference_f < mean(sim_df$y_rep_uncrtnty)
##
eq_a_a[s] <- equation_a < posterior_equation_a[s]
eq_a_b[s] <- equation_b < posterior_equation_a[s]
eq_a_c[s] <- reference_c < posterior_equation_a[s]
eq_a_d[s] <- reference_d < posterior_equation_a[s]
eq_a_e[s] <- reference_e < posterior_equation_a[s]
eq_a_f[s] <- reference_f < posterior_equation_a[s]
##
eq_b_a[s] <- equation_a < posterior_equation_b[s]
eq_b_b[s] <- equation_b < posterior_equation_b[s]
eq_b_c[s] <- reference_c < posterior_equation_b[s]
eq_b_d[s] <- reference_d < posterior_equation_b[s]
eq_b_e[s] <- reference_e < posterior_equation_b[s]
eq_b_f[s] <- reference_f < posterior_equation_b[s]
}
## Calculate posterior predictive p-values:
p_stat_mean_ref_gr_gaussian_a[r] <- mean(stat_mean_ref_gr_gaussian_a)
p_stat_mean_ref_gr_gaussian_b[r] <- mean(stat_mean_ref_gr_gaussian_b)
p_stat_mean_ref_gr_gaussian_c[r] <- mean(stat_mean_ref_gr_gaussian_c)
p_stat_mean_ref_gr_gaussian_d[r] <- mean(stat_mean_ref_gr_gaussian_d)
p_stat_mean_ref_gr_gaussian_e[r] <- mean(stat_mean_ref_gr_gaussian_e)
p_stat_mean_ref_gr_gaussian_f[r] <- mean(stat_mean_ref_gr_gaussian_f)
##
p_stat_mean_ref_gr_uncrtnty_a[r] <- mean(stat_mean_ref_gr_uncrtnty_a)
p_stat_mean_ref_gr_uncrtnty_b[r] <- mean(stat_mean_ref_gr_uncrtnty_b)
p_stat_mean_ref_gr_uncrtnty_c[r] <- mean(stat_mean_ref_gr_uncrtnty_c)
p_stat_mean_ref_gr_uncrtnty_d[r] <- mean(stat_mean_ref_gr_uncrtnty_d)
p_stat_mean_ref_gr_uncrtnty_e[r] <- mean(stat_mean_ref_gr_uncrtnty_e)
p_stat_mean_ref_gr_uncrtnty_f[r] <- mean(stat_mean_ref_gr_uncrtnty_f)
##
p_stat_mean_sim_df_gaussian_a[r] <- mean(stat_mean_sim_df_gaussian_a)
p_stat_mean_sim_df_gaussian_b[r] <- mean(stat_mean_sim_df_gaussian_b)
p_stat_mean_sim_df_gaussian_c[r] <- mean(stat_mean_sim_df_gaussian_c)
p_stat_mean_sim_df_gaussian_d[r] <- mean(stat_mean_sim_df_gaussian_d)
p_stat_mean_sim_df_gaussian_e[r] <- mean(stat_mean_sim_df_gaussian_e)
p_stat_mean_sim_df_gaussian_f[r] <- mean(stat_mean_sim_df_gaussian_f)
##
p_stat_mean_sim_df_uncrtnty_a[r] <- mean(stat_mean_sim_df_uncrtnty_a)
p_stat_mean_sim_df_uncrtnty_b[r] <- mean(stat_mean_sim_df_uncrtnty_b)
p_stat_mean_sim_df_uncrtnty_c[r] <- mean(stat_mean_sim_df_uncrtnty_c)
p_stat_mean_sim_df_uncrtnty_d[r] <- mean(stat_mean_sim_df_uncrtnty_d)
p_stat_mean_sim_df_uncrtnty_e[r] <- mean(stat_mean_sim_df_uncrtnty_e)
p_stat_mean_sim_df_uncrtnty_f[r] <- mean(stat_mean_sim_df_uncrtnty_f)
##
p_stat_mean_eq_a_a[r] <- mean(eq_a_a)
p_stat_mean_eq_a_b[r] <- mean(eq_a_b)
p_stat_mean_eq_a_c[r] <- mean(eq_a_c)
p_stat_mean_eq_a_d[r] <- mean(eq_a_d)
p_stat_mean_eq_a_e[r] <- mean(eq_a_e)
p_stat_mean_eq_a_f[r] <- mean(eq_a_f)
##
p_stat_mean_eq_b_a[r] <- mean(eq_b_a)
p_stat_mean_eq_b_b[r] <- mean(eq_b_b)
p_stat_mean_eq_b_c[r] <- mean(eq_b_c)
p_stat_mean_eq_b_d[r] <- mean(eq_b_d)
p_stat_mean_eq_b_e[r] <- mean(eq_b_e)
p_stat_mean_eq_b_f[r] <- mean(eq_b_f)
if (r %% 50 < .5) {cat(".\n")} else {cat(".")} ## Progress 'bar'
}Organize results
results_holdout_ppc <- rbind(data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' = "exp(b0+b1)",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_gaussian_a),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' = "exp(b0+b1)",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_uncrtnty_a),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' = "exp(b0+b1+.5*sigma_gamma^2)",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_gaussian_b),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' = "exp(b0+b1+.5*sigma_gamma^2)",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_uncrtnty_b),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' = "exp(b0+b1)",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_gaussian_a),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' = "exp(b0+b1)",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_uncrtnty_a),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' = "exp(b0+b1+.5*sigma_gamma^2)",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_gaussian_b),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' = "exp(b0+b1+.5*sigma_gamma^2)",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_uncrtnty_b),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' =
"mean of prior pred. on ref. grid",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_gaussian_c),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' =
"mean of prior pred. on ref. grid",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_uncrtnty_c),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' =
"mean of prior pred. on sim. data",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_gaussian_d),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' =
"mean of prior pred. on sim. data",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_uncrtnty_d),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' =
"mean of prior pred. on ref. grid",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_gaussian_c),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' =
"mean of prior pred. on ref. grid",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_uncrtnty_c),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' =
"mean of prior pred. on sim. data",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_gaussian_d),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' =
"mean of prior pred. on sim. data",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_uncrtnty_d),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' =
"mean of prior pred. on ref. grid (uncertainty)",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_gaussian_e),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' =
"mean of prior pred. on ref. grid (uncertainty)",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_uncrtnty_e),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' =
"mean of prior pred. on sim. data (uncertainty)",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_gaussian_f),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' =
"mean of prior pred. on sim. data (uncertainty)",
'posterior_predict_population' = "ref. grid",
'value' = p_stat_mean_ref_gr_uncrtnty_f),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' =
"mean of prior pred. on ref. grid (uncertainty)",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_gaussian_e),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' =
"mean of prior pred. on ref. grid (uncertainty)",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_uncrtnty_e),
data.frame('brms_sample_new_levels' = "gaussian",
'use_prior' =
"mean of prior pred. on sim. data (uncertainty)",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_gaussian_f),
data.frame('brms_sample_new_levels' = "uncertainty",
'use_prior' =
"mean of prior pred. on sim. data (uncertainty)",
'posterior_predict_population' = "sim. data",
'value' = p_stat_mean_sim_df_uncrtnty_f),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1)]",
'use_prior' = "exp(b0+b1)",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_a_a),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1)]",
'use_prior' = "exp(b0+b1+.5*sigma_gamma^2)",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_a_b),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1+.5*sigma_gamma^2)]",
'use_prior' = "exp(b0+b1)",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_b_a),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1+.5*sigma_gamma^2)]",
'use_prior' = "exp(b0+b1+.5*sigma_gamma^2)",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_b_b),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1)]",
'use_prior' = "prior_pred_ref_gr_gaussian",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_a_c),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1+.5*sigma_gamma^2)]",
'use_prior' = "prior_pred_ref_gr_gaussian",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_b_c),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1)]",
'use_prior' = "prior_pred_sim_df_gaussian",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_a_d),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1+.5*sigma_gamma^2)]",
'use_prior' = "prior_pred_sim_df_gaussian",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_b_d),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1)]",
'use_prior' = "prior_pred_ref_gr_uncrtnty",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_a_e),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1+.5*sigma_gamma^2)]",
'use_prior' = "prior_pred_ref_gr_uncrtnty",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_b_e),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1)]",
'use_prior' = "prior_pred_sim_df_uncrtnty",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_a_f),
data.frame('brms_sample_new_levels' =
"none [exp(b0+b1+.5*sigma_gamma^2)]",
'use_prior' = "prior_pred_sim_df_uncrtnty",
'posterior_predict_population' = "none",
'value' = p_stat_mean_eq_b_f))Visualise QOI-Check
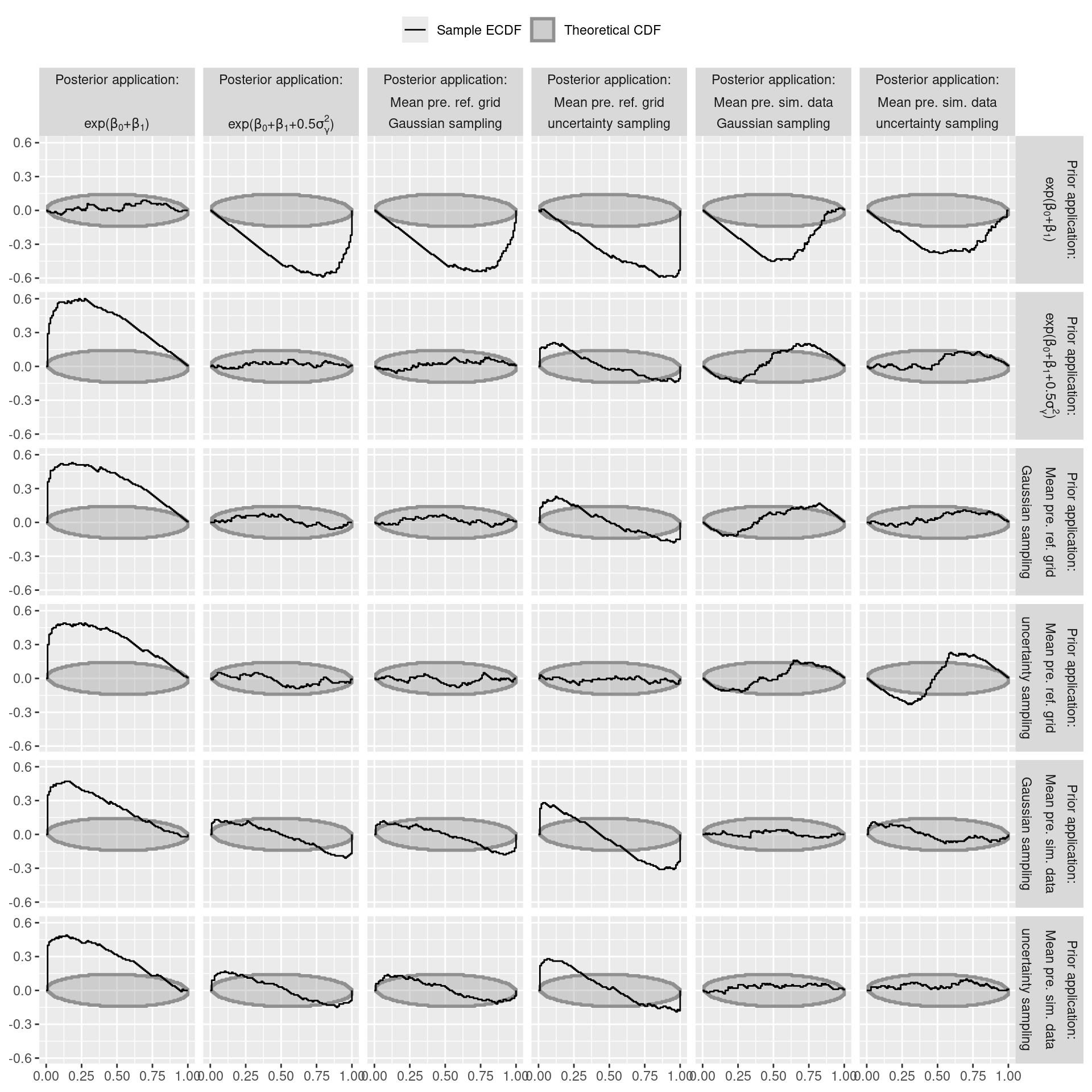
tmp <- results_holdout_ppc
tmp$variable <- paste0("Mean of prediction on ",
tmp$posterior_predict_population, " with\n",
tmp$brms_sample_new_levels, " sampling for gamma.\n",
"Prior application: ", tmp$use_prior)
tmp$variable <- gsub(x = tmp$variable, pattern = "gaussian",
replacement = "Gaussian", fixed = T)
tmp$rank <- tmp$value * 1000
tmp$max_rank <- 1000
tmp$sim_id <- rep(1:100, 6 * 6)
tmp <- dat_ecdf_diff(x = tmp)
tmp$ecdf_df$x1 <- sapply(X = strsplit(x = tmp$ecdf_df$variable, split = '\n',
fixed = T), FUN = function(x){x[1]})
tmp$ecdf_df$x2 <- sapply(X = strsplit(x = tmp$ecdf_df$variable, split = '\n',
fixed = T), FUN = function(x){x[2]})
tmp$ecdf_df$x3 <- sapply(X = strsplit(x = tmp$ecdf_df$variable, split = '\n',
fixed = T), FUN = function(x){x[3]})
tmp$ecdf_df$x3 <- gsub(x = tmp$ecdf_df$x3, pattern = "Prior application: ",
replacement = "", fixed = T)
tmp$ecdf_df$x3f <- as.factor(tmp$ecdf_df$x3)
tmp$ecdf_df$x4f <- as.factor(tmp$ecdf_df$x3)
levels(tmp$ecdf_df$x3f) <- c(expression("exp(" * beta[0] * "+" * beta[1] * ")"),
expression("exp(" * beta[0] * "+" * beta[1] *
"+0.5" * sigma[gamma]^2 * ")"),
expression(paste("Mean pre. ref. grid")),
expression(paste("Mean pre. ref. grid")),
expression(paste("Mean pre. sim. data")),
expression(paste("Mean pre. sim. data")),
expression(paste("Mean pre. ref. grid")),
expression(paste("Mean pre. ref. grid")),
expression(paste("Mean pre. sim. data")),
expression(paste("Mean pre. sim. data")))
levels(tmp$ecdf_df$x4f) <- c("",
"",
"Gaussian sampling",
"uncertainty sampling",
"Gaussian sampling",
"uncertainty sampling",
"Gaussian sampling",
"uncertainty sampling",
"Gaussian sampling",
"uncertainty sampling")
tmp$ecdf_df$x1a <- "Posterior application:"
tmp$ecdf_df$x3a <- "Prior application:"
tmp$ecdf_df$x1[tmp$ecdf_df$x1 == "Mean of prediction on none with"] <- " "
tmp$ecdf_df$x1f <- as.factor(tmp$ecdf_df$x1)
levels(tmp$ecdf_df$x1f) <- c(" ",
"Mean pre. ref. grid",
"Mean pre. sim. data")
tmp$ecdf_df$x2[tmp$ecdf_df$x2 == "none [exp(b0+b1)] sampling for gamma."] <-
"exp(b0+b1)"
tmp$ecdf_df$x2[tmp$ecdf_df$x2 ==
"none [exp(b0+b1+.5*sigma_gamma^2)] sampling for gamma."] <-
"exp(b0+b1+.5*sigma_gamma^2)"
tmp$ecdf_df$x2f <- as.factor(tmp$ecdf_df$x2)
levels(tmp$ecdf_df$x2f) <- c(expression("exp(" * beta[0] * "+" * beta[1] * ")"),
expression("exp(" * beta[0] * "+" * beta[1] *
"+0.5" * sigma[gamma]^2 * ")"),
expression(paste("Gaussian sampling")),
expression(paste("uncertainty sampling")))
col_color <- col_fill <-
c(colorspace::sequential_hcl(n = 20, pal = "Grays")[10], "black")
names(col_color) <- names(col_fill) <-
c("theoretical CDF", "sample ECDF")
l <- c('theoretical CDF' = expression("Theoretical CDF"),
'sample ECDF' = expression("Sample ECDF"))
ggplot(tmp$ecdf_df, aes(color = type, fill = type)) +
geom_ribbon(data = tmp$limits_df_trans,
aes(x = x, ymax = ymax, ymin = ymin), alpha = .33,
linewidth = 1) +
geom_step(aes(x = z, y = z_diff, group = variable)) +
scale_color_manual(name = "", values = col_color, labels = l) +
scale_fill_manual(name = "", values = col_fill, labels = l) +
scale_alpha_identity() +
xlab(NULL) +
ylab(NULL) +
facet_grid(cols = vars(x1a, x1f, x2f),
rows = vars(x3a, x3f, x4f),
labeller = labeller(x2f = label_parsed,
x3f = label_parsed)) +
theme(strip.text = element_text(margin = margin(b = 0, t = 0))) +
theme(legend.position = "top")
References
Allaire, J. J., Teague, C., Scheidegger, C., Xie, Y., & Dervieux, C. (2024). Quarto (Version 1.4.553). https://doi.org/10.5281/zenodo.5960048
Bengtsson, H. (2021). A unifying framework for parallel and distributed processing in r using futures. The R Journal, 13(2), 208–227. https://doi.org/10.32614/RJ-2021-048
Bürkner, P.-C. (2017). brms: An R package for Bayesian multilevel models using Stan. Journal of Statistical Software, 80(1), 1–28. https://doi.org/10.18637/jss.v080.i01
Bürkner, P.-C. (2018). Advanced Bayesian multilevel modeling with the R package brms. The R Journal, 10(1), 395–411. https://doi.org/10.32614/RJ-2018-017
Bürkner, P.-C. (2021). Bayesian item response modeling in R with brms and Stan. Journal of Statistical Software, 100(5), 1–54. https://doi.org/10.18637/jss.v100.i05
Gabry, J., Češnovar, R., Johnson, A., & Bronder, S. (2024). Cmdstanr: R interface to ’CmdStan’. https://mc-stan.org/cmdstanr/
Li, J., & Huggins, J. H. (2024). Calibrated model criticism using split predictive checks. https://arxiv.org/abs/2203.15897
Modrák, M., Moon, A. H., Kim, S., Bürkner, P., Huurre, N., Faltejsková, K., Gelman, A., & Vehtari, A. (2023). Simulation-based calibration checking for bayesian computation: The choice of test quantities shapes sensitivity. Bayesian Analysis, Advance publication. https://doi.org/10.1214/23-BA1404
R Core Team. (2024). R: A Language and Environment for Statistical Computing (Version 4.4.1). R Foundation for Statistical Computing.
Stauffer, R., Mayr, G. J., Dabernig, M., & Zeileis, A. (2009). Somewhere over the rainbow: How to make effective use of colors in meteorological visualizations. Bulletin of the American Meteorological Society, 96(2), 203–216. https://doi.org/10.1175/BAMS-D-13-00155.1
Wickham, H. (2016). ggplot2: Elegant graphics for data analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org