Prior-Posterior Derived-Predictive Consistency Checks for Post-Estimation Calculated Quantities of Interest (*QOI-Check*)

Holger Sennhenn-Reulen\textsuperscript{\orcidlink{0000-0002-4782-4387}} \linebreak \textsuperscript{Northwest German Forest Research Institute (NW-FVA), Germany.}

Intro

Relevant parts of the code given here is inspired by the resources of the great SBC package (Modrák et al., 2023) published at https://hyunjimoon.github.io/SBC/index.html.

Also, coding of posterior p-values is inspired by the split predictive check (Li & Huggins, 2024) R code published at https://github.com/TARPS-group/split-predictive-checks.

Software

We use the statistical software environment R (R Core Team, 2024), and R add-on packages SBC (Modrák et al., 2023), brms (Bürkner, 2017, 2018, 2021), mgcv (Wood, 2011), cmdstanr (Gabry et al., 2024), ggplot2 (Wickham, 2016), colorspace (Stauffer et al., 2009), and future (Bengtsson, 2021).

This document is produced using Quarto (Allaire et al., 2024).

Organize R Session

Load packages:

library("mgcv")
library("SBC")
library("brms")
library("cmdstanr")
library("ggplot2")
library("colorspace")
library("cowplot")
library("future")

Settings:

rm(list = ls())
options(brms.backend = "cmdstanr")
# Using parallel processing
plan(multisession)
options(SBC.min_chunk_size = 5)
# Setup caching of results
cache_dir <- "./SBC_cache"
if(!dir.exists(cache_dir)) {
  dir.create(cache_dir)
}

Data preparation function for graphical uniformity checks:

# convenient wrapper around mgcv::PredictMat
PredictMat <- function(object, data, ...) {
  data <- rm_attr(data, "terms")
  out <- mgcv::PredictMat(object, data = data, ...)
  if (length(dim(out)) < 2L) {
    # fixes issue #494
    out <- matrix(out, nrow = 1)
  }
  out
}
# convenient wrapper around mgcv::smoothCon
smoothCon <- function(object, data, ...) {
  data <- rm_attr(data, "terms")
  vars <- setdiff(c(object$term, object$by), "NA")
  for (v in vars) {
    if (is_like_factor(data[[v]])) {
      # allow factor-like variables #562
      data[[v]] <- as.factor(data[[v]])
    } else if (inherits(data[[v]], "difftime")) {
      # mgcv cannot handle 'difftime' variables
      data[[v]] <- as.numeric(data[[v]])
    }
  }
  mgcv::smoothCon(object, data = data, ...)
}
# Aid prediction from smooths represented as 'type = 2'
# code obtained from the doc of ?mgcv::smooth2random
# @param sm output of mgcv::smoothCon
# @param re output of mgcv::smooth2random
# @param data new data supplied for prediction
# @return A list of the same structure as returned by mgcv::smooth2random
s2rPred <- function(sm, re, data) {
  #sm = sm[[1]] ## for check!
  #re = hmmmm ## for check!
  #data = nd ## for check!
  # prediction matrix for new data
  X <- mgcv::PredictMat(sm, data)
  # transform to RE parameterization
  if (!is.null(re$trans.U)) {
    X <- X %*% re$trans.U
  }
  if (is.null(re$trans.D)) {
    # regression spline without penalization
    out <- list(Xf = X)
  } else {
    X <- t(t(X) * re$trans.D)
    # re-order columns according to random effect re-ordering
    X[, re$rind] <- X[, re$pen.ind != 0]
    # re-order penalization index in same way
    pen.ind <- re$pen.ind
    pen.ind[re$rind] <- pen.ind[pen.ind > 0]
    # start returning the object
    Xf <- X[, which(re$pen.ind == 0), drop = FALSE]
    out <- list(rand = list(), Xf = Xf)
    for (i in seq_along(re$rand)) {
      # loop over random effect matrices
      out$rand[[i]] <- X[, which(pen.ind == i), drop = FALSE]
      attr(out$rand[[i]], "s.label") <- attr(re$rand[[i]], "s.label")
    }
    names(out$rand) <- names(re$rand)
  }
  out
}

Data preparation function for graphical uniformity checks:

## from https://github.com/TeemuSailynoja/simultaneous-confidence-bands/tree/main
dat_ecdf_diff <- function (x, variables = NULL, K = NULL, 
                           gamma = NULL, prob = 0.95, 
                           combine_variables = NULL, 
                           ecdf_alpha = NULL, ..., 
                           parameters = NULL) {
  if (!is.null(parameters)) {
    warning("The `parameters` argument is deprecated use `variables` instead.")
    if (is.null(variables)) {
      variables <- parameters
    }
  }
  ecdf_data <- data_for_ecdf_plots(x, variables = variables,
                                   prob = prob, K = K, gamma = gamma, 
                                   combine_variables = combine_variables,
                                   ecdf_alpha = ecdf_alpha, ...)
  if (ecdf_data$N < 50 && is.null(K)) {
    message("With less than 50 simulations, we recommend using plot_ecdf as it has better fidelity.\n",
            "Disable this message by explicitly setting the K parameter. ",
            "You can use the strings \"max\" (high fidelity) or \"min\" (nicer plot) or choose a specific integer.")
  }
  N <- ecdf_data$N
  K <- ecdf_data$K
  z <- ecdf_data$z
  ecdf_df <- dplyr::mutate(ecdf_data$ecdf_df, z_diff = ecdf -
                             z, type = "sample ECDF")
  limits_df_trans <- dplyr::mutate(ecdf_data$limits_df, 
                                   ymax = upper - uniform_val, 
                                   ymin = lower - uniform_val, 
                                   type = "theoretical CDF")
  return(list('ecdf_df' = ecdf_df,
              'limits_df_trans' = limits_df_trans))
}

Data Generator

f_generate_y <- function(sim_df, 
                         eta, 
                         sigma) {
  sim_df$'mu_y' <- eta
  sim_df$'sigma_y' <- rep(sigma, nrow(sim_df))
  sim_df$'y' <- rnorm(n = nrow(sim_df), 
                      mean = sim_df$'mu_y', 
                      sd = sim_df$'sigma_y')
  return(sim_df)
}
f_generate_xz <- function(N, b_Intercept, phi) {
  mu <- plogis(b_Intercept)
  return(rbeta(n = N, shape1 = mu * phi, shape2 = (1 - mu) * phi))
}
f_generate_one_sim <- function(N) {
  prior_mu <- list('b_x_Intercept' = 0, 
                   'b_z_Intercept' = -1.1,
                   'b_y_Intercept' = .5,
                   'bs_y_sxz_1' = 1,
                   'bs_y_sxz_2' = -1,
                   'sds_y_sxz_1' = 1,
                   'phi_x' = 3,
                   'phi_z' = 3,
                   'sigma_y' = .1)
  prior_sd <- list('b_x_Intercept' = .001, 
                   'b_z_Intercept' = .001,
                   'b_y_Intercept' = .1,
                   'bs_y_sxz_1' = .1,
                   'bs_y_sxz_2' = .1,
                   'sds_y_sxz_1' = .1,
                   'phi_x' = .001,
                   'phi_z' = .001,
                   'sigma_y' = .01)
  b_y_Intercept <- rnorm(n = 1, 
                         mean = prior_mu$b_y_Intercept, 
                         sd = prior_sd$b_y_Intercept)
  bs_y_sxz_1 <- rnorm(n = 1, 
                      mean = prior_mu$bs_y_sxz_1, 
                      sd = prior_sd$bs_y_sxz_1)
  bs_y_sxz_2 <- rnorm(n = 1, 
                      mean = prior_mu$bs_y_sxz_2, 
                      sd = prior_sd$bs_y_sxz_2)
  sds_y_sxz_1 <- rnorm(n = 1, 
                       mean = prior_mu$sds_y_sxz_1, 
                       sd = prior_sd$sds_y_sxz_1)
  sds_y_sxz_1 <- abs(sds_y_sxz_1)
  sigma_y <- rnorm(n = 1, 
                   mean = prior_mu$sigma_y, 
                   sd = prior_sd$sigma_y)
  b_x_Intercept <- rnorm(n = 1, 
                         mean = prior_mu$b_x_Intercept, 
                         sd = prior_sd$b_x_Intercept)
  phi_x <- rnorm(n = 1, 
                 mean = prior_mu$phi_x, 
                 sd = prior_sd$phi_x)
  phi_x <- abs(phi_x)
  b_z_Intercept <- rnorm(n = 1, 
                         mean = prior_mu$b_z_Intercept, 
                         sd = prior_sd$b_z_Intercept)
  phi_z <- rnorm(n = 1, 
                 mean = prior_mu$phi_z, 
                 sd = prior_sd$phi_z)
  phi_z <- abs(phi_z)
  x <- f_generate_xz(N, b_x_Intercept, phi_x)
  z <- f_generate_xz(N, b_z_Intercept, phi_z)
  dat_xz <- data.frame('x' = x, 'z' = z)
  sm <- mgcv::smoothCon(object = s(x, z, k = 10), data = dat_xz,
                        absorb.cons = TRUE, modCon = 3, diagonal.penalty = TRUE)
  sm2r <- mgcv::smooth2random(object = sm[[1]], vnames = c('x', 'z'), type = 2)
  Xf <- sm2r[['Xf']]
  Xr <- sm2r[['rand']][['Xr']]
  s_y_sxz <- t(MASS::mvrnorm(n = 1, mu = rep(0, ncol(Xr)), 
                             Sigma = sds_y_sxz_1 * diag(ncol(Xr))))
  variables <- list('b_y_Intercept' = b_y_Intercept, 
                    'bs_y_sxz_1' = bs_y_sxz_1, 
                    'bs_y_sxz_2' = bs_y_sxz_2,
                    'sds_y_sxz_1' = sds_y_sxz_1,
                    's_y_sxz[1]' = s_y_sxz[1, 1], 
                    's_y_sxz[2]' = s_y_sxz[1, 2], 
                    's_y_sxz[3]' = s_y_sxz[1, 3],
                    's_y_sxz[4]' = s_y_sxz[1, 4],
                    's_y_sxz[5]' = s_y_sxz[1, 5],
                    's_y_sxz[6]' = s_y_sxz[1, 6],
                    's_y_sxz[7]' = s_y_sxz[1, 7],
                    'sigma_y' = sigma_y,
                    'b_x_Intercept' = b_x_Intercept, 
                    'b_z_Intercept' = b_z_Intercept,
                    'phi_x' = phi_x,
                    'phi_z' = phi_z)
  etaf <- Xf %*% c(bs_y_sxz_1, bs_y_sxz_2)
  etar <- Xr %*% t(s_y_sxz)
  eta <- b_y_Intercept + etaf + etar
  return(list('variables' = variables,
              'generated' = f_generate_y(sim_df = dat_xz, 
                                         eta = eta, 
                                         sigma = sigma_y)))
}
f_generate_n_sims <- SBC_generator_function(f_generate_one_sim, 
                                            N = 1000)
set.seed(123)
datasets <- generate_datasets(f_generate_n_sims, 20)
head(datasets$generated[[1]])

          x           z      mu_y   sigma_y          y
1 0.6428125 0.471219239 0.3496019 0.1012929 0.33045945
2 0.1542820 0.158118671 0.1796588 0.1012929 0.10296001
3 0.3846568 0.116883626 0.1478711 0.1012929 0.22810111
4 0.3718601 0.228222288 0.2942474 0.1012929 0.43050453
5 0.4644184 0.003815211 0.1276784 0.1012929 0.05732729
6 0.6761364 0.082005730 1.0524761 0.1012929 1.00740764

Backend

priors <- prior(normal(.5,.1), class = "Intercept", resp = "y") +
  prior(normal(1,.1), class = "b", coef = "sxz_1", resp = "y") +
  prior(normal(-1,.1), class = "b", coef = "sxz_2", resp = "y") +
  prior(normal(1,.1), class = "sds", resp = "y") +
  prior(normal(.1,.01), class = "sigma", resp = "y") +
  prior(normal(0,.001), class = "Intercept", resp = "x") +
  prior(normal(-1.1,.001), class = "Intercept", resp = "z") +
  prior(normal(3,.001), class = "phi", resp = "x") +
  prior(normal(3,.001), class = "phi", resp = "z")
frmla <- bf(x ~ 1, family = Beta(link = "logit")) +
  bf(z ~ 1, family = Beta(link = "logit")) +
  bf(y ~ s(x, z, k = 10), family = gaussian())
f_backend <- SBC_backend_brms(frmla,
                              prior = priors, 
                              chains = 1,
                              iter = 2000,
                              template_data = datasets$generated[[1]],
                              out_stan_file = file.path(cache_dir, 
                                                               "case_study_II.stan"))

set.seed(0)
results <- compute_SBC(datasets = datasets, 
                       backend = f_backend, 
                       cache_mode = "results", 
                       cache_location = file.path(cache_dir,
                                                        "SBC_results_case_study_II"))

Visualize bivariate smooth at first four simulation runs

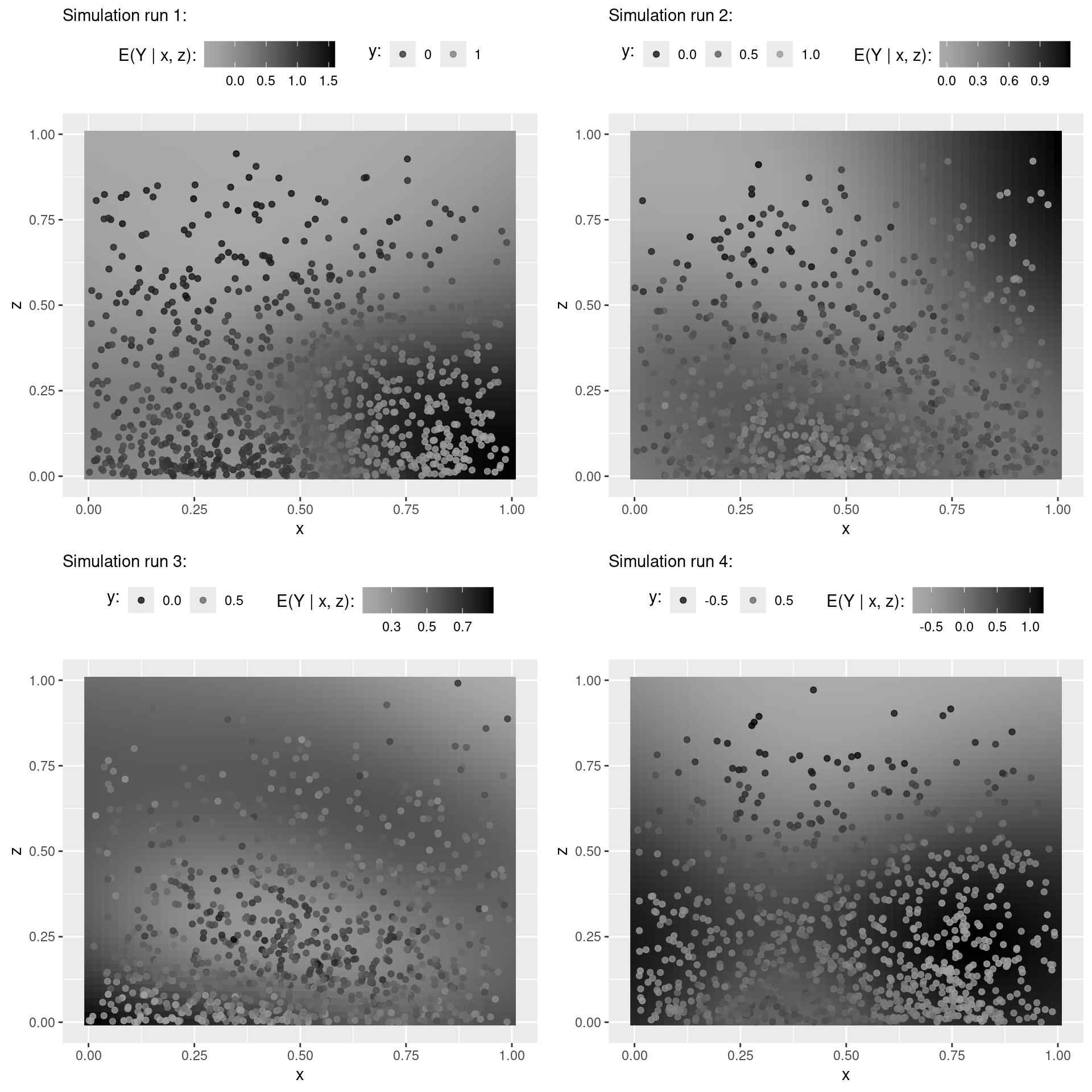
nd <- expand.grid('x' = seq(0, 1, by = .02), 'z' = seq(0, 1, by = .02))
p_list <- vector("list", 4)
for (r in 1:4) {
  m <- results$fits[[r]]
  fit <- fitted(object = m, newdata = nd)
  nd$fit_y <- fit[, 'Estimate', 'y']
  p_list[[r]] <- ggplot(data = nd, aes(x = x, y = z)) + 
    geom_raster(aes(fill = fit_y)) + 
    scale_fill_continuous_sequential(pal = "Grays", l1 = 0, l2 = 70) +
    geom_point(data = m$data, aes(color = y), alpha = .8) + 
    scale_color_continuous_sequential(breaks = scales::breaks_extended(n = 3), 
                                      pal = "Grays", l1 = 0, l2 = 70, rev = FALSE) +
    # colorspace::scale_color_continuous_sequential(pal = "Rocket") +
    guides(color = guide_legend(nrow = 1)) +
    labs(color = "y:", fill = "E(Y | x, z):", 
         subtitle = paste0("Simulation run ", r, ":")) +
    theme(legend.position = 'top') +
    theme(legend.title = element_text(vjust = .8))
}
cowplot::plot_grid(plotlist = p_list, ncol = 2)

QOI-Check

f_postprocessing <- function(m, b, focus_on = 'x', at = .8, 
                             integration_grid = seq(.025, .975, by = .05)) {
  if (!(focus_on %in% c('x', 'z'))) {
    stop("'focus_on' must be either 'x' or 'z'.")
  }
  nd <- data.frame('variable1' = at)
  nd <- as.data.frame(expand.grid('variable1' = nd$variable1, 
                                  'variable2' = integration_grid))
  names(nd) <- c('x', 'z')
  fit <- fitted(m, newdata = nd, dpar = "mu", summary = F)
  if (focus_on == 'x') {
    phi <- fitted(m, newdata = nd, resp = "z", dpar = "phi", summary = F)
    shape1 <- fit[, , "z"] * phi
    shape2 <- (1 - fit[, , "z"]) * phi
    d <- shape1 * 0
    for (i in 1:nrow(nd)) {
      d[, i] <- dbeta(x = nd$z[i], shape1 = shape1[, i], shape2 = shape2[, i])
    }
  }
  if (focus_on == 'z') {
    phi <- fitted(m, newdata = nd, resp = "x", dpar = "phi", summary = F)
    shape1 <- fit[, , "x"] * phi
    shape2 <- (1 - fit[, , "x"]) * phi
    d <- shape1 * 0
    for (i in 1:nrow(nd)) {
      d[, i] <- dbeta(x = nd$x[i], shape1 = shape1[, i], shape2 = shape2[, i])
    }
  }
  d <- d / apply(d, MAR = 1, FUN = sum)
  tmp <- abs(apply(d, MAR = 1, FUN = sum) - 1)
  if (any(tmp > 1e-10)) {
    stop("No proper calculation of weights!")
  }
  return(list('Weighted' = apply(d * fit[, , 'y'], MAR = 1, FUN = sum), 
              'Unweighted' = apply(fit[, , 'y'], MAR = 1, FUN = mean)))
}
ranks_rgpp <- NULL
for (j in 1:20) {
  cat(paste0("j = ", j, ":\n"))
  cat("  f_postprocessing_fast():\n")
  cat("  ")
  res <- all_weighted <- NULL
  x_grid <- seq(.025, .975, by = .05)
  for (i in 1:length(x_grid)) {
    x <- x_grid[i]
    tmp <- f_postprocessing(results$fits[[j]], 
                            as.data.frame(datasets$variables)[j, ], 
                            focus_on = 'x', x, 
                            seq(.0005, .9995, by = .001))
    all_weighted <- cbind(all_weighted, tmp[['Weighted']])
    for (method in c('Weighted', 'Unweighted')) {
      res <- rbind(res, 
                   data.frame('x' = x, 
                              'y' = mean(tmp[[method]]), 
                              'method' = method, 
                              'stat' = 'Mean'))
      res <- rbind(res, 
                   data.frame('x' = x, 
                              'y' = median(tmp[[method]]), 
                              'method' = method, 
                              'stat' = 'Median'))
      res <- rbind(res, 
                   data.frame('x' = x, 
                              'y' = quantile(tmp[[method]], probs = .025), 
                              'method' = method, 
                              'stat' = '2.5% quantile'))
      res <- rbind(res, 
                   data.frame('x' = x, 
                              'y' = quantile(tmp[[method]], probs = .975), 
                              'method' = method, 
                              'stat' = '97.5% quantile'))
    }
    cat(".")
  }
  res0 <- res
  ## Compare to GAM s() + s() + ti()
  ## https://cran.r-project.org/web/packages/mgcv/mgcv.pdf
  ## p. 79:
  ## "Sometimes it is interesting to specify smooth models with a main 
  ##  effects + interaction structure such as
  ##  E(yi) = f1(xi) + f2(zi) + f3(xi, zi)
  ##  [...]
  ##  for example. 
  ##  Such models should be set up using ti terms in the model formula. 
  ##  For example:
  ##  y ~ ti(x) + ti(z) + ti(x,z), 
  ##  [...]
  ##  The ti terms produce interactions with the component main effects 
  ##  excluded appropriately. (There is in fact no need to use ti terms 
  ##  for the main effects here, s terms could also be used.)"                                                        ## "[...] in fact no need to use ti terms for the main effects here, 
  ##  s terms could also be used."
  m_gam <- gam(y ~ s(x) + s(z) + ti(x, z), data = datasets$generated[[j]])
  nd <- data.frame(x = x_grid, z = x_grid)
  tmp <- predict(m_gam, type = "terms", newdata = nd)
  res <- rbind(res, 
               data.frame(x = x_grid, 
                          y = tmp[, 's(x)'] + coef(m_gam)[1], 
                          method = "mgcv::gam: s(x) [model: y ~ s(x) + s(z) + ti(x, z)]", 
                          stat = "Effect"))
  ## ############################################
  ## Reference grid posterior predictive check ##
  ## ############################################
  cat("\n")
  cat("  reference grid prior prediction:\n")
  cat("  ")
  x_grid <- seq(.025, .975, by = .05)
  ref_grid_prior_mean_y_x <- rep(NA, length(x_grid))
  for (i in 1:length(x_grid)) {
    b <- as.data.frame(datasets$variables)[j, ]
    z <- f_generate_xz(N = 10000, 
                       b_Intercept = as.numeric(b['b_z_Intercept']), 
                       phi = as.numeric(b['phi_z']))
    dat_xz <- data.frame('x' = x_grid[i], 'z' = z)
    sm <- mgcv::smoothCon(object = s(x, z, k = 10), data = results$fits[[j]]$data,
                          absorb.cons = TRUE, modCon = 3, diagonal.penalty = TRUE)
    sm2r <- mgcv::smooth2random(object = sm[[1]], vnames = c('x', 'z'), type = 2)
    sm2r_pre <- s2rPred(sm = sm[[1]], re = sm2r, data = dat_xz)
    Xf <- sm2r_pre[['Xf']]
    Xr <- sm2r_pre[['rand']][['Xr']]
    etaf <- Xf %*% as.numeric(b[grep(names(b), pattern = "bs_", fixed = T)])
    etar <- Xr %*% as.numeric(b[grep(names(b), pattern = "s_y_sxz[", fixed = T)])
    eta <- as.numeric(b['b_y_Intercept']) + etaf + etar
    dat_xz <- f_generate_y(dat_xz, as.numeric(eta), as.numeric(b["sigma_y"]))
    ref_grid_prior_mean_y_x[i] <- mean(dat_xz$y)
    cat(".")
  }
  cat("\n")
  res <- rbind(res, 
               data.frame(x = x_grid, 
                          y = ref_grid_prior_mean_y_x,
                          method = "Reference grid prior prediction (N = 1000)", 
                          stat = "Mean"))
  res$stat <- factor(res$stat, levels = c("Mean", "Median", "2.5% quantile", 
                                          "97.5% quantile", "Effect"))
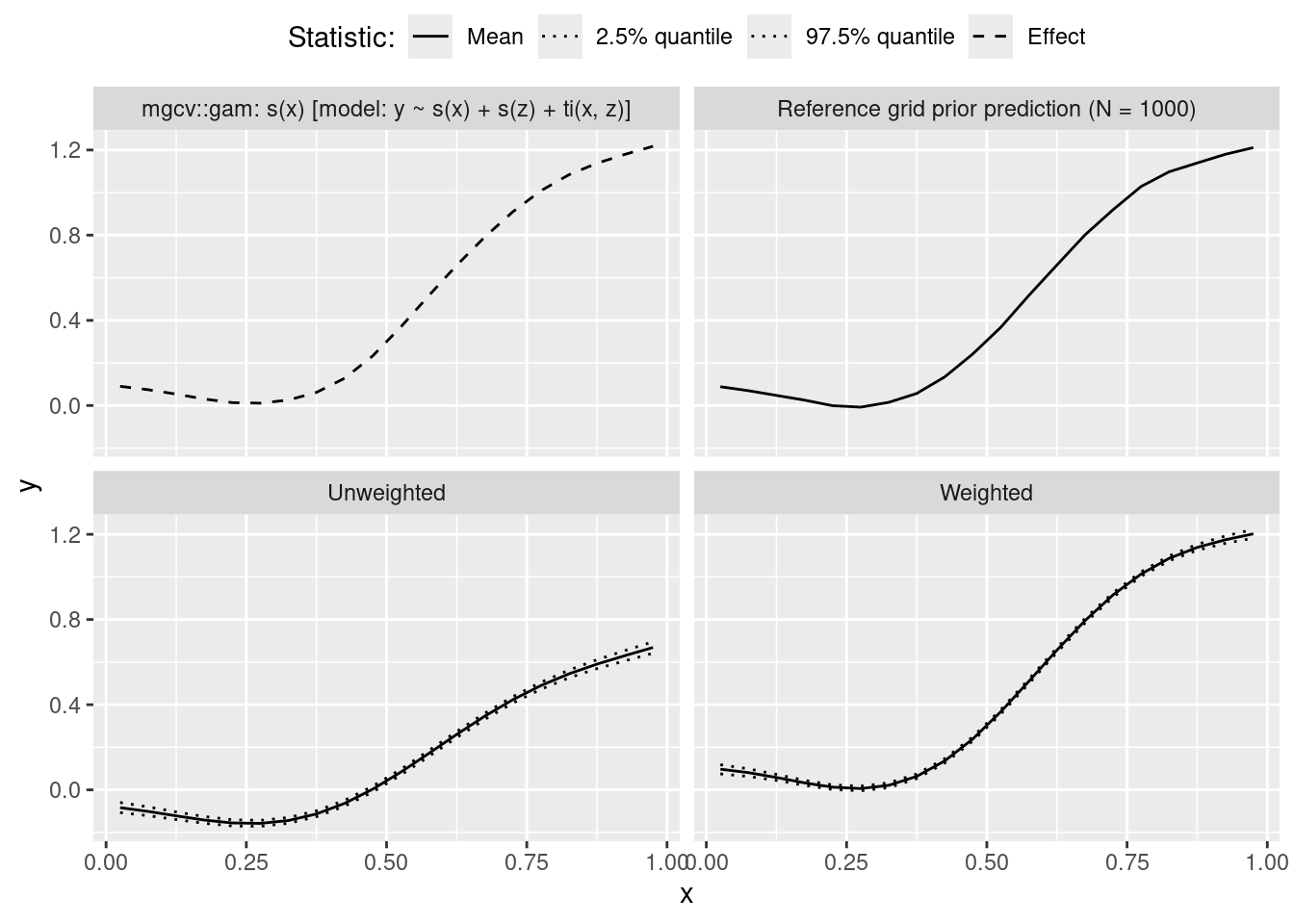
  if (j == 1) {
  p <- ggplot(data = subset(res, stat != "Median"), aes(x = x, y = y)) + 
    geom_line(aes(group = paste0(stat, method), 
                  linetype = stat)) + #, color = method
    theme(legend.position = "top", legend.box="vertical", legend.margin=margin()) +
    guides(color = "none") +
    scale_linetype_manual(values = c(1, 3, 3, 2)) +
    facet_wrap(~ method) +
    labs(color = "Method:", linetype = "Statistic:")
  }
  rgpp_all_weighted <- rbind(subset(res, 
                           method == "reference grid prior prediction (N = 1000)")$y, 
                           all_weighted)
  ranks_rgpp <- cbind(ranks_rgpp, 
                      apply(rgpp_all_weighted, MAR = 2, 
                            FUN = function(x){mean(x[-1] > x[1])}))
}
ranks <- data.frame('rank' = reshape2::melt(ranks_rgpp)$value, 
                    'max_rank' = 1,
                    'variable' = reshape2::melt(ranks_rgpp)$Var1,
                    'sim_id' = reshape2::melt(ranks_rgpp)$Var2)
ranks$rank <- ranks$rank * 1000
ranks$rank <- ranks$rank - 1 + runif(nrow(ranks))
ranks$max_rank <- ranks$max_rank * 1000
ranks$variable <- factor(paste("x:", x_grid[ranks$variable]), 
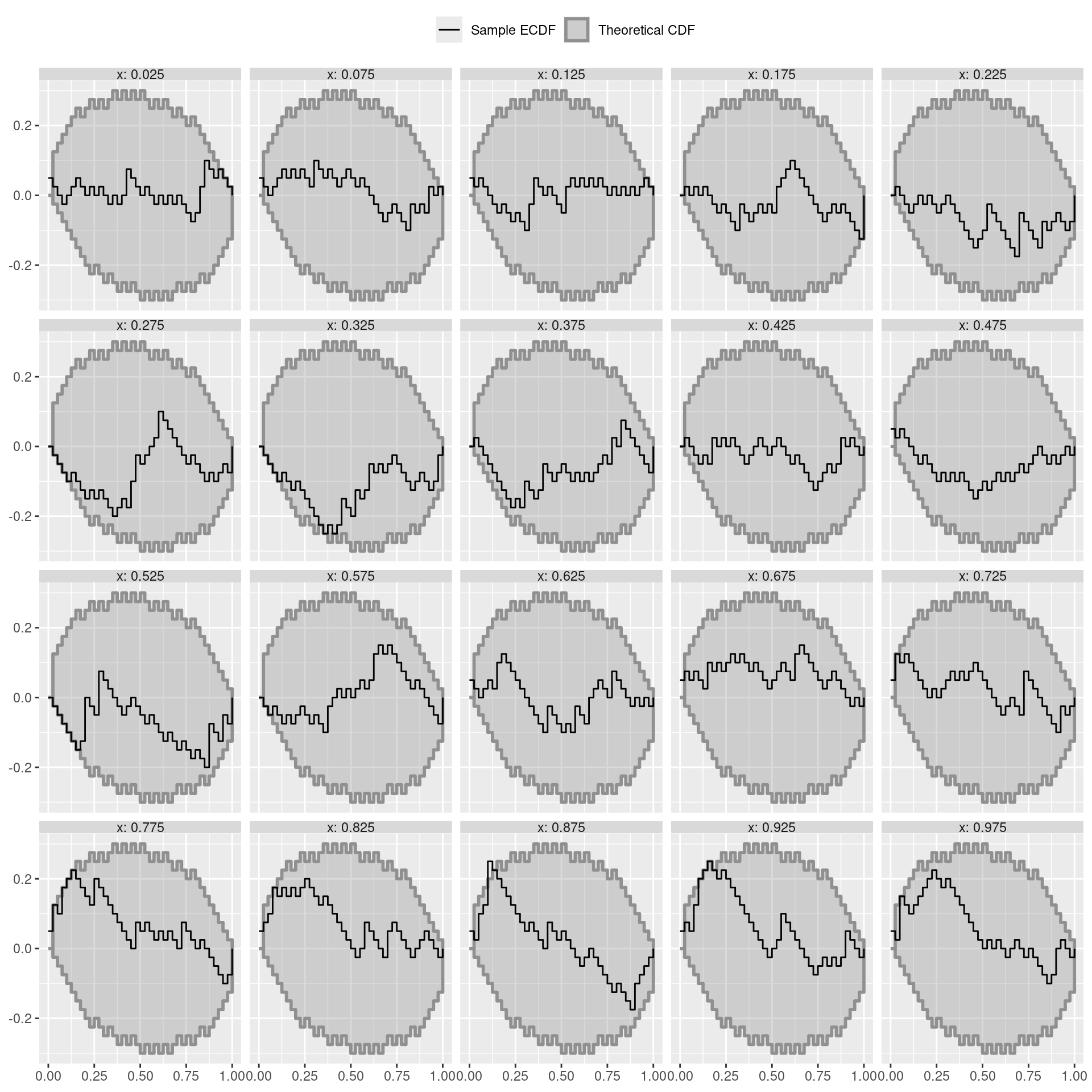
                         levels = paste("x:", x_grid))

tmp <- dat_ecdf_diff(ranks, variables = levels(ranks$variable), K = 40)
col_color <- c(colorspace::sequential_hcl(n = 20, pal = "Grays")[10], "black")
col_fill <- c(colorspace::sequential_hcl(n = 20, pal = "Grays")[10], "black")
names(col_color) <- names(col_fill) <- 
    c("theoretical CDF", "sample ECDF")
l <- c('theoretical CDF' = expression("Theoretical CDF"), 
       'sample ECDF' = expression("Sample ECDF"))
ggplot(tmp$ecdf_df, aes(color = type, fill = type)) + 
  geom_ribbon(data = tmp$limits_df_trans, 
              aes(x = x, ymax = ymax, ymin = ymin), alpha = .33, 
              linewidth = 1) + 
  geom_step(aes(x = z, y = z_diff, group = variable)) + 
  scale_color_manual(name = "", values = col_color, labels = l) + 
  scale_fill_manual(name = "", values = col_fill, labels = l) + 
  scale_alpha_identity() + 
  xlab(NULL) + 
  ylab(NULL) + 
  facet_wrap(~variable) +
  theme(strip.text = element_text(margin = margin(b = 0, t = 0))) +
  theme(legend.position = "top")

Visualise ‘isolated effect’ of `x` for 1st simulation run

print(p)

References

Allaire, J. J., Teague, C., Scheidegger, C., Xie, Y., & Dervieux, C. (2024). Quarto (Version 1.4.553). https://doi.org/10.5281/zenodo.5960048

Bengtsson, H. (2021). A unifying framework for parallel and distributed processing in r using futures. The R Journal, 13(2), 208–227. https://doi.org/10.32614/RJ-2021-048

Bürkner, P.-C. (2017). brms: An R package for Bayesian multilevel models using Stan. Journal of Statistical Software, 80(1), 1–28. https://doi.org/10.18637/jss.v080.i01

Bürkner, P.-C. (2018). Advanced Bayesian multilevel modeling with the R package brms. The R Journal, 10(1), 395–411. https://doi.org/10.32614/RJ-2018-017

Bürkner, P.-C. (2021). Bayesian item response modeling in R with brms and Stan. Journal of Statistical Software, 100(5), 1–54. https://doi.org/10.18637/jss.v100.i05

Gabry, J., Češnovar, R., Johnson, A., & Bronder, S. (2024). Cmdstanr: R interface to ’CmdStan’. https://mc-stan.org/cmdstanr/

Li, J., & Huggins, J. H. (2024). Calibrated model criticism using split predictive checks. https://arxiv.org/abs/2203.15897

Modrák, M., Moon, A. H., Kim, S., Bürkner, P., Huurre, N., Faltejsková, K., Gelman, A., & Vehtari, A. (2023). Simulation-based calibration checking for bayesian computation: The choice of test quantities shapes sensitivity. Bayesian Analysis, Advance publication. https://doi.org/10.1214/23-BA1404

R Core Team. (2024). R: A Language and Environment for Statistical Computing (Version 4.4.1). R Foundation for Statistical Computing.

Stauffer, R., Mayr, G. J., Dabernig, M., & Zeileis, A. (2009). Somewhere over the rainbow: How to make effective use of colors in meteorological visualizations. Bulletin of the American Meteorological Society, 96(2), 203–216. https://doi.org/10.1175/BAMS-D-13-00155.1

Wickham, H. (2016). ggplot2: Elegant graphics for data analysis. Springer-Verlag New York. https://ggplot2.tidyverse.org

Wood, S. N. (2011). Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society (B), 73(1), 3–36.