All contents are licensed under CC BY-NC-ND 4.0.

1 Objectives of control structures.

‘Automation’ of the repetition of structurally identical commands.

  • Repetition of a command – with objects remaining the same, or changing – with a predetermined or flexible number of repetitions.
  • Conditional execution of various tasks.
  • Generalization of tasks by defining functions.

2 Logical comparisons.

Command TRUE if:
== Equality
!= Inequality
>, >= Left side greater than (or equal to) the right side
<, <= Left side less than (or equal to) the right side
%in% Is left side included in vector on right side?
  • all() returns TRUE if all elements of the vector are TRUE.
  • any() returns TRUE if at least one element of the vector is TRUE.
  • is.na() and is.null() return TRUE if the respective object (e.g. element of a vector) is NA or NULL.
  • A logical value can be negated with a preceding ! (e.g. !TRUE is FALSE)
  • which() returns the index set (as an integer vector) if the logical comparison resulted in TRUE.

2.1 Exercises

is.na(drought$bair)
any(is.na(drought$bair))
drought$bair > 0
all(drought$bair > 0)
drought$bair > 1
any(drought$bair > 1)
all(drought$bair > 1)
which(drought$bair > 1)
drought$bair[which(drought$bair > 1)]
(tmp <- round(drought$bair, 1))
c(.8, 1.2) %in% tmp
c(.8, 1.2) %in% drought$bair
which(tmp %in% c(.8, 1.2))
drought$bair[which(tmp %in% c(.8, 1.2))]
tmp <- c(drought$bair[1:5], NA)
all(tmp > 0)
any(is.na(tmp))
which(is.na(tmp))
all(tmp[-which(is.na(tmp))] > 0)
mean(tmp)
mean(tmp, na.rm = T)

3 Conditional execution

3.1 if () { } else { }

Usage:

if (condition) {
  ... ## Commands if condition is TRUE
} else {
  ... ## Commands if condition is FALSE
}
  • TRUE or FALSE condition necessary.
  • ‘if-else’-sequences can be nested within one another.

Applied example together with the next topic.

3.1.1 Exercises

a <- drought$bair[1]
if (a > 1) {
  print("a is greater than 1.")
} else {
  print("a is not greater than 1.")
}
index <- 2
tmp <- rep(NA, nrow(drought))
if (drought$bair[index] < 1) {
  result <- "bair<1"
  if (drought$elev[index] < 1000) {
    tmp[index] <- paste0("1_", result, ",elev<1000")
  } else {
    tmp[index] <- paste0("2_", result, ",elev>=1000")
  }
} else {
  result <- "bair>=1"
  if (drought$elev[index] < 1000) {
    tmp[index] <- paste0("3_", result, ",elev<1000")
  } else {
    tmp[index] <- paste0("4_", result, ",elev>=1000")
  }
}
tmp

3.2 for-loops

for loops often offer a simple and pragmatic way to complete steps in data management / preparation.

Usage:

for (index in vector) {
  ... index ... ## Commands that in some form depend on index.
}
  • New object index runs all elements in vector.
  • index remains constant during ... index ...
  • index jumps to the next (if available) value of vector after running through ... index ....
  • index takes each value of vector once.
  • The number of iterations of ... index ... is determined by the length of vector.

3.2.1 Exercises

library("ggplot2")
tmp1 <- frost$bud_burst_days_since_may1st
tmp2 <- frost$end_1st_dev_stage_days_since_may1st
days_since_may1st <- min(tmp1):max(tmp2)
rm(tmp1, tmp2)
p <- ggplot(data = frost, aes(x = year, y = bud_burst_days_since_may1st)) + 
  ylim(range(days_since_may1st))
for (index in 1:nrow(frost)) {
  tmp_x <- rep(frost$year[index], times = 2)
  tmp_y <- c(frost$bud_burst_days_since_may1st[index], 
             frost$end_1st_dev_stage_days_since_may1st[index])
  p <- p + geom_line(data = data.frame(x = tmp_x, y = tmp_y), 
                     aes(x = x, y = y))
}
p

3.3 Example of a for loop with if

The goal of this example is to get to know which day in May is the one at which a young Douglas fir was most often in the first development stage.

As a preparation, we nee to set up a data-frame as the object that will carry the result:

tmp1 <- frost$bud_burst_days_since_may1st
tmp2 <- frost$end_1st_dev_stage_days_since_may1st
days_since_may1st <- min(tmp1):max(tmp2)
rm(tmp1, tmp2)
res <- data.frame(days_since_may1st = days_since_may1st, 
                  n_at_risk = NA)

3.3.1 Illustrating the loop index

The for-loop will run through our resulting data-frame res, line by line. We can try and illustrate this with the following graph, where the x-axis carries the values of the loop-index, and the y-axis the value of the days_since_may1st variable that will be taken in each of the loop’s ... index ... circles.

library("colorspace")
## 
## Attache Paket: 'colorspace'
## Das folgende Objekt ist maskiert 'package:spatstat.geom':
## 
##     coords
ggplot(data = data.frame(x = 1:nrow(res), 
                         y = res$days_since_may1st), 
       aes(x = x, y = y)) + 
  geom_point(aes(color = x)) + 
  scale_color_continuous_divergingx(pal = "Zissou", mid = nrow(res)/2) + 
  labs(x = "for-loop index 'index'", y = "res$days_since_may1st at 'index'")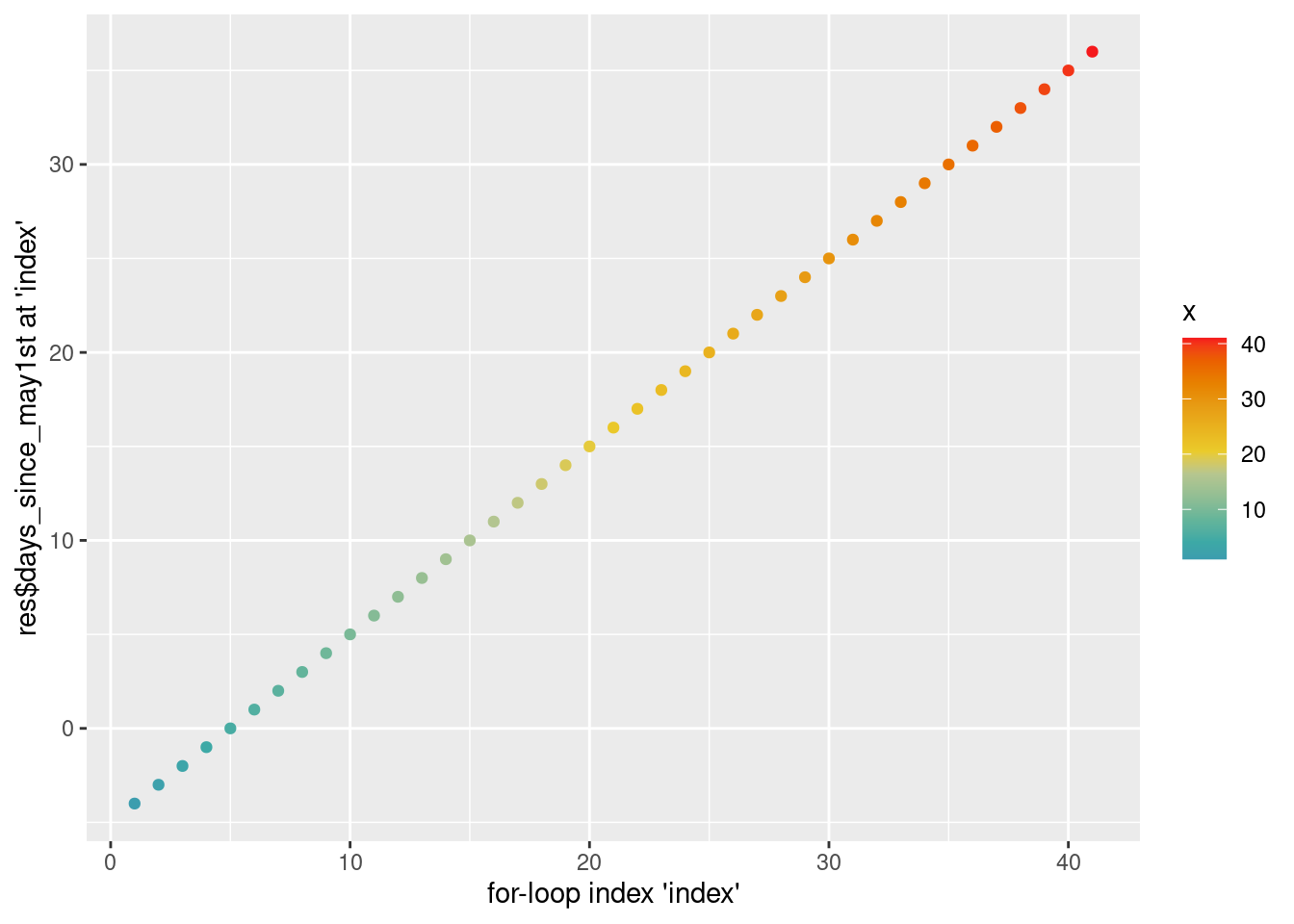

3.3.2 An iteration ‘by hand’

We can run a first iteration by hand that does what ... index ... should do in our loop: compare the current – at index = 1– res$days_since_may1st value to each of the first development stage periods that are given by frost$bud_burst_days_since_may1stand frost$end_1st_dev_stage_days_since_may1st. If any of those periods covers our current day, than at least a value of 1 will result for res$n_at_risk[index].

index <- 1
# re-use 'p' from for-loop exercises
p <- p + geom_hline(yintercept = res$days_since_may1st[index], linetype = 2)
## boolean 1 and 2:
bool1 <- frost$bud_burst_days_since_may1st <= res$days_since_may1st[index]
bool2 <- frost$end_1st_dev_stage_days_since_may1st >= res$days_since_may1st[index]
## if any ... else ...
if (any(bool1 & bool2)) {
  which_true <- which(bool1 & bool2)
  p <- p + geom_point(data = data.frame(x = frost$year[which_true], 
                                        y = rep(days_since_may1st[index], 
                                                times = length(which_true))),
                      aes(x = x, y = y, color = y))# , col = paint[index], pch = 16)
  res$n_at_risk[index] <- length(which_true)
} else {
  res$n_at_risk[index] <- 0
}
p + scale_color_continuous_divergingx(pal = "Zissou", mid = nrow(res)/2)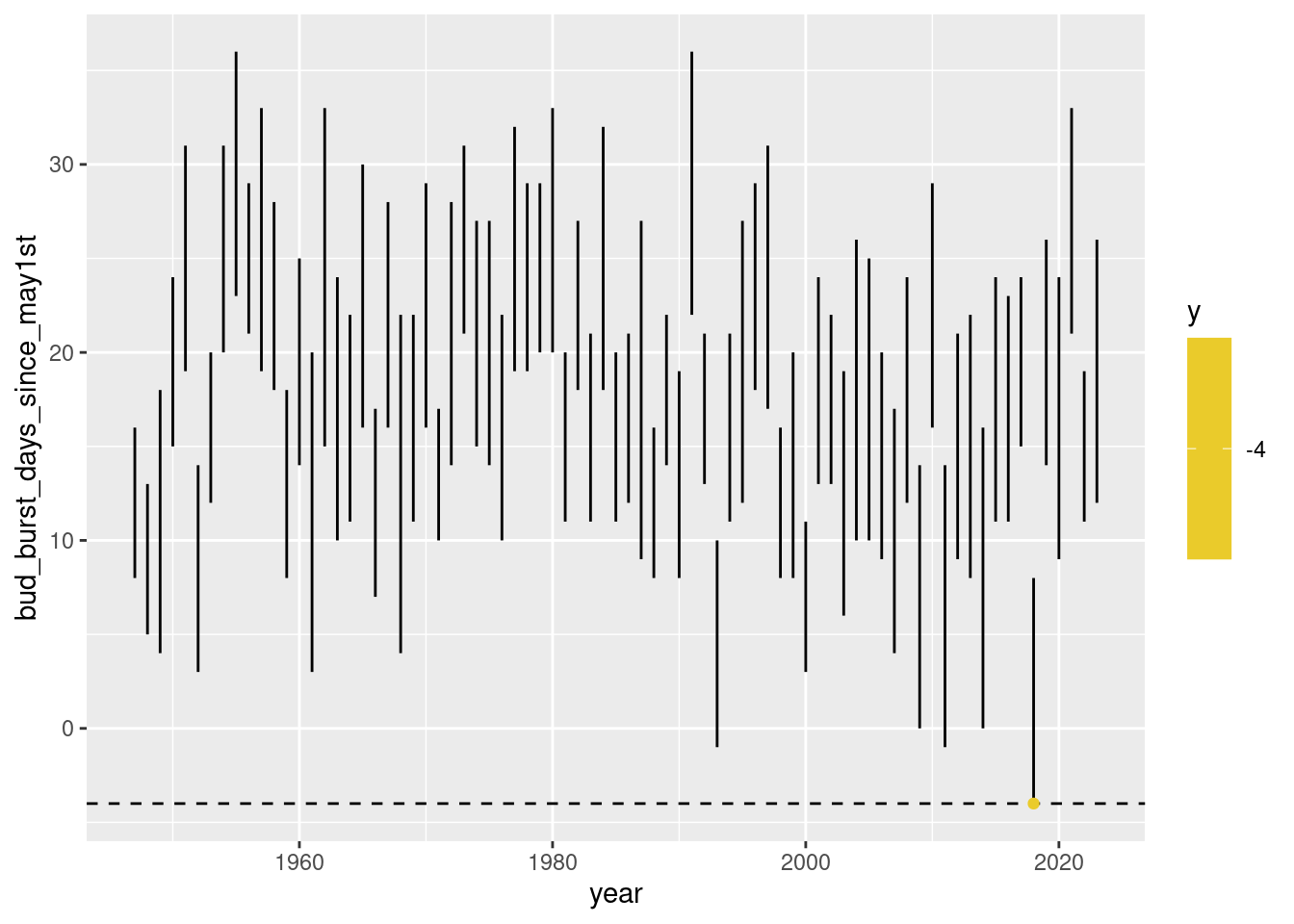

rm(index)

3.3.3 The ‘full’ loop

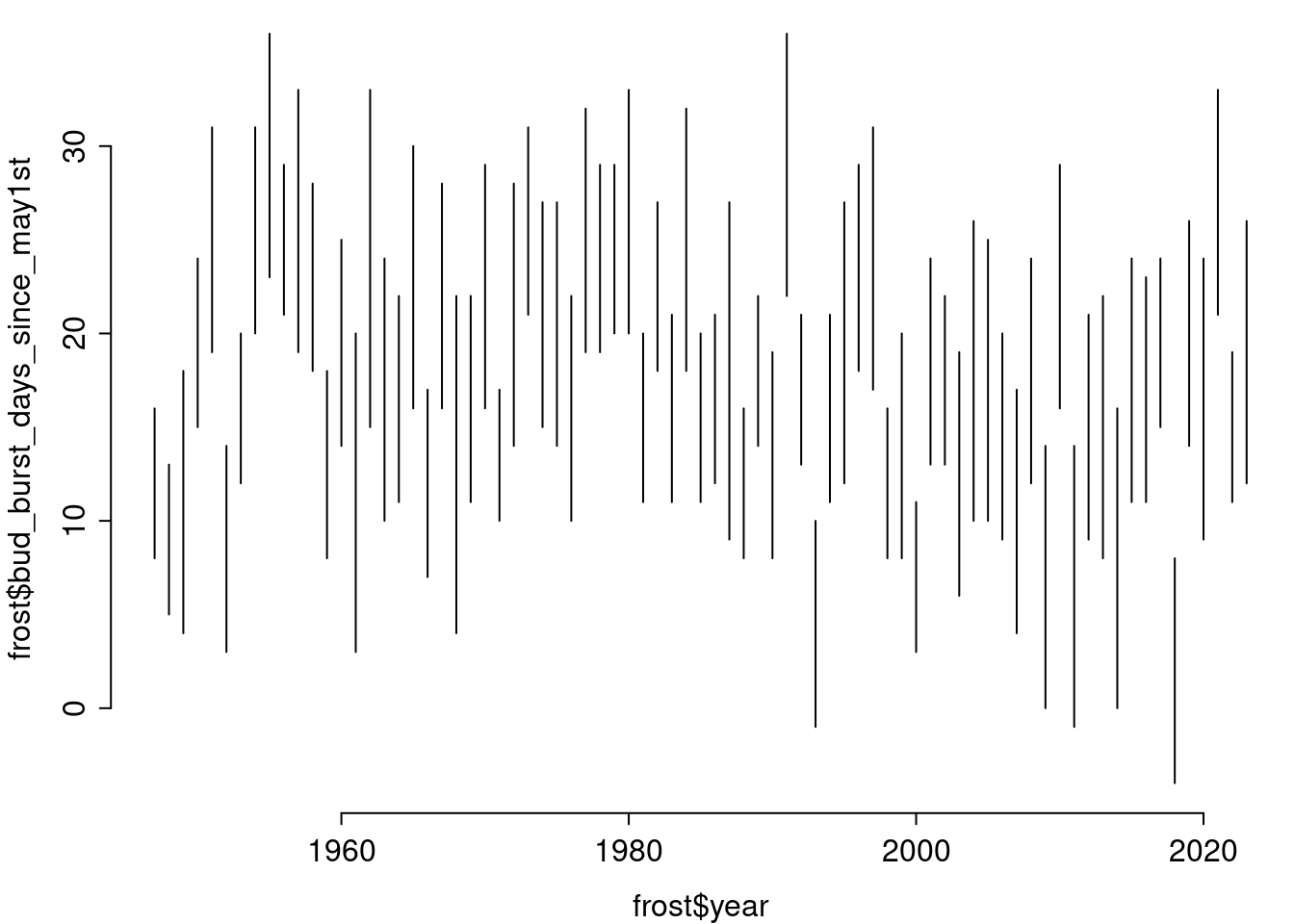
Now we just take what we have implemented before and – by using for (index in 1:nrow(res)) { effortlessly run through all the lines of res.

par(mar = c(3, 3, .1, .1), mgp = c(2, .5, 0), tcl = -.3)
plot(frost$year, frost$bud_burst_days_since_may1st, type = "n",
     ylim = range(days_since_may1st), bty = "n")
for (index in 1:nrow(frost)) { ## here, the uninteresting loop
  tmp_x <- rep(frost$year[index], times = 2)
  tmp_y <- c(frost$bud_burst_days_since_may1st[index], 
             frost$end_1st_dev_stage_days_since_may1st[index])
  lines(x = tmp_x, y = tmp_y)
}

for (index in 2:nrow(res)) { ## let 'index' begin here at 2 since index = 1 already perfomr
  p <- p + geom_hline(yintercept = res$days_since_may1st[index], linetype = 2)
  ## boolean 1 and 2:
  bool1 <- frost$bud_burst_days_since_may1st <= res$days_since_may1st[index]
  bool2 <- frost$end_1st_dev_stage_days_since_may1st >= res$days_since_may1st[index]
  ## if any ... else ...
  if (any(bool1 & bool2)) {
    which_true <- which(bool1 & bool2)
    p <- p + geom_point(data = data.frame(x = frost$year[which_true], 
                                          y = rep(days_since_may1st[index], 
                                                  times = length(which_true))),
                        aes(x = x, y = y, color = y))# , col = paint[index], pch = 16)
    res$n_at_risk[index] <- length(which_true)
  } else {
    res$n_at_risk[index] <- 0
  }
}
p + scale_color_continuous_divergingx(pal = "Zissou", mid = nrow(res)/2)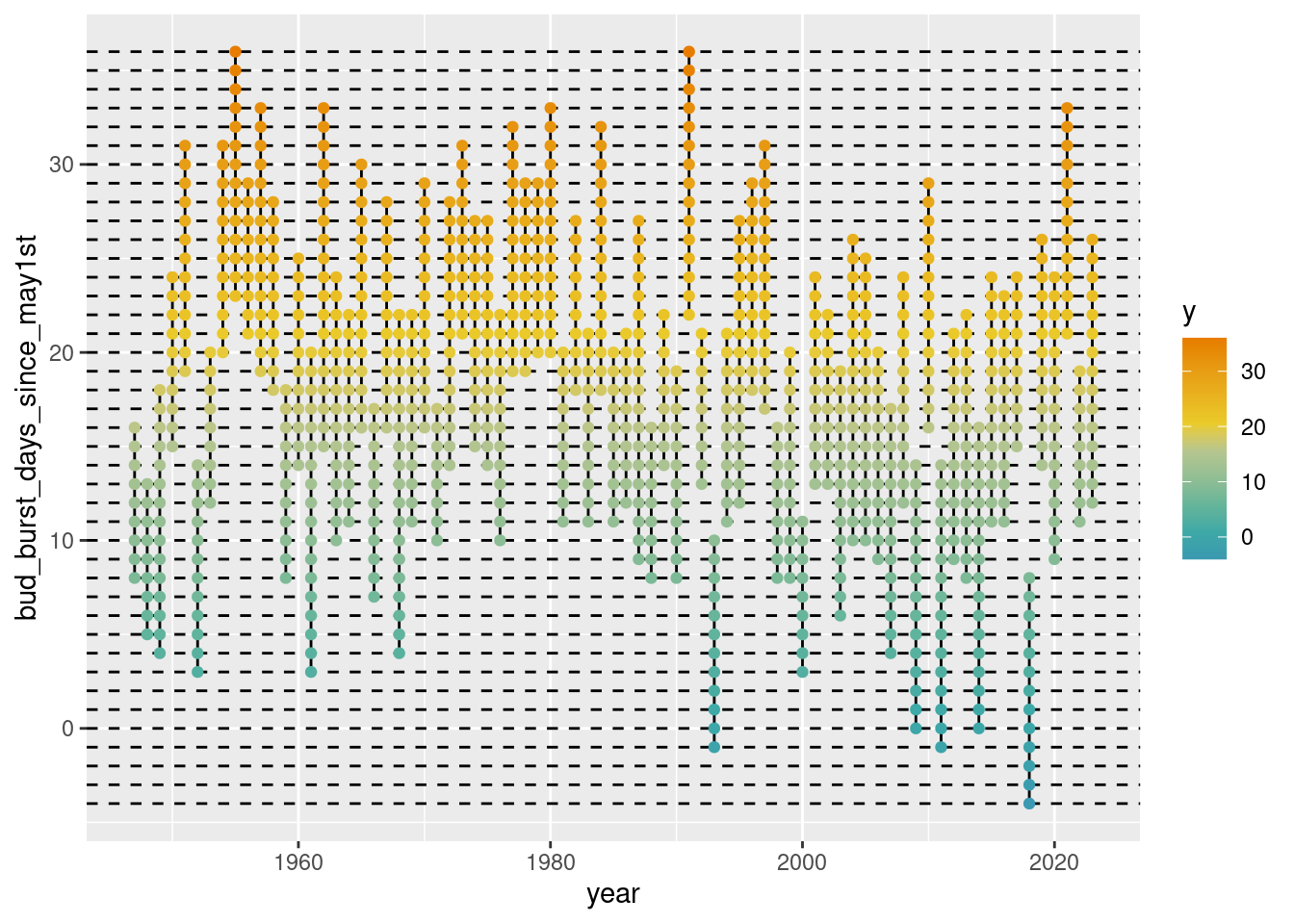

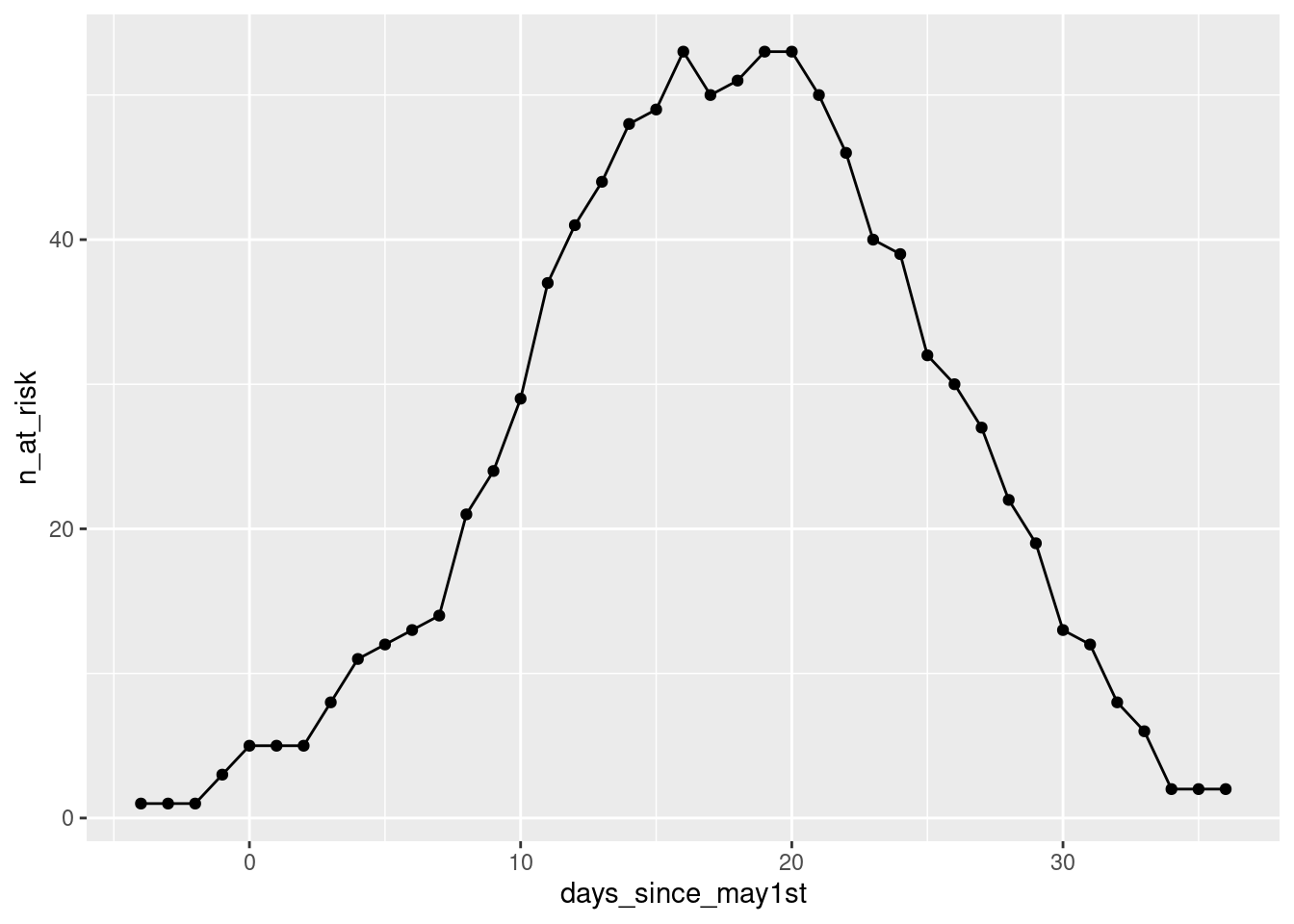
ggplot(data = res, aes(x = days_since_may1st, y = n_at_risk)) + 
  geom_line() + 
  geom_point()

3.4 while-loops.

while loops are used less often in data management / preparation, but are more likely to be found in computationally intensive applications (e.g. for optimization).

Usage:

index <- k ## 'k' here has to be smaller than 'K' in next line.
while (index < K){
  ...
  index <- index + 1
}
  • The commands that ’... stands for, and the following line, are repeated as long as the condition is TRUE (i.e. here as long as k\(<\)K).
  • flexible number of repetitions.
  • stops immediately after the condition – index < K in the above usage example – is no longer met, ie. is FALSE for the first time.

The following two examples are two applications of a while-loop that came into my mind. They might be a bit too distracting from the goals of ‘Introduction to R’, so feel completely free to skip them …

3.4.1 Example 1

This example does Bayesian inference for a simple one parameter model – estimation of an unknown quantity which is a proportion between \(0\) and \(1\) – by filtering the prior proposals that lead to the simulated data that are equal to the data sample – the likelihood works as some sort of sieve here.

accepted <- 0
xtabs(~ (frost$n_frost > .5))
## frost$n_frost > 0.5
## FALSE  TRUE 
##    65    12
prior <- post <- NULL
while (accepted < 1000) {
  p <- rbeta(n = 1, shape1 = 1/3, shape2 = 1/3) ## http://dx.doi.org/10.1214/11-EJS648
  prior <- c(prior, p)
  y_tilde <- sample(x = c(TRUE, FALSE), size = nrow(frost), replace = T, 
                    prob = c(p, 1 - p))
  if (sum(y_tilde) == sum(frost$n_frost > .5)) {
    accepted <- accepted + 1
    post <- c(post, p)
  }
}
length(post)
## [1] 1000
length(prior)
## [1] 107145
length(post) / length(prior)
## [1] 0.009333147
summary(post)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## 0.05909 0.13177 0.16001 0.16135 0.18938 0.29381
summary(prior)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## 0.00000 0.08274 0.50072 0.50018 0.91782 1.00000
tmp <- rbind(data.frame(value = post, 
                        k = "posterior"),
             data.frame(value = prior, 
                        k = "prior"))
ggplot(data = tmp, aes(x = value, group = k, fill = k)) + 
  geom_histogram(aes(y = after_stat(density)), alpha = .8, position = "identity", 
                 binwidth = .05, center = .025) + 
  scale_fill_discrete_qualitative(pal = "Dark 2", rev = T) + 
  theme(legend.position = "top") + 
  geom_vline(xintercept = sum(frost$n_frost > .5) / nrow(frost), linewidth = 2, linetype = 2) + 
  geom_vline(xintercept = median(post), linewidth = 1, linetype = 1) +
  labs(x = "Probability", y = "Density", fill = NULL, 
       caption = "Dashed vertical line is at empirical mean.\nSolid vertical line is at posterior median.")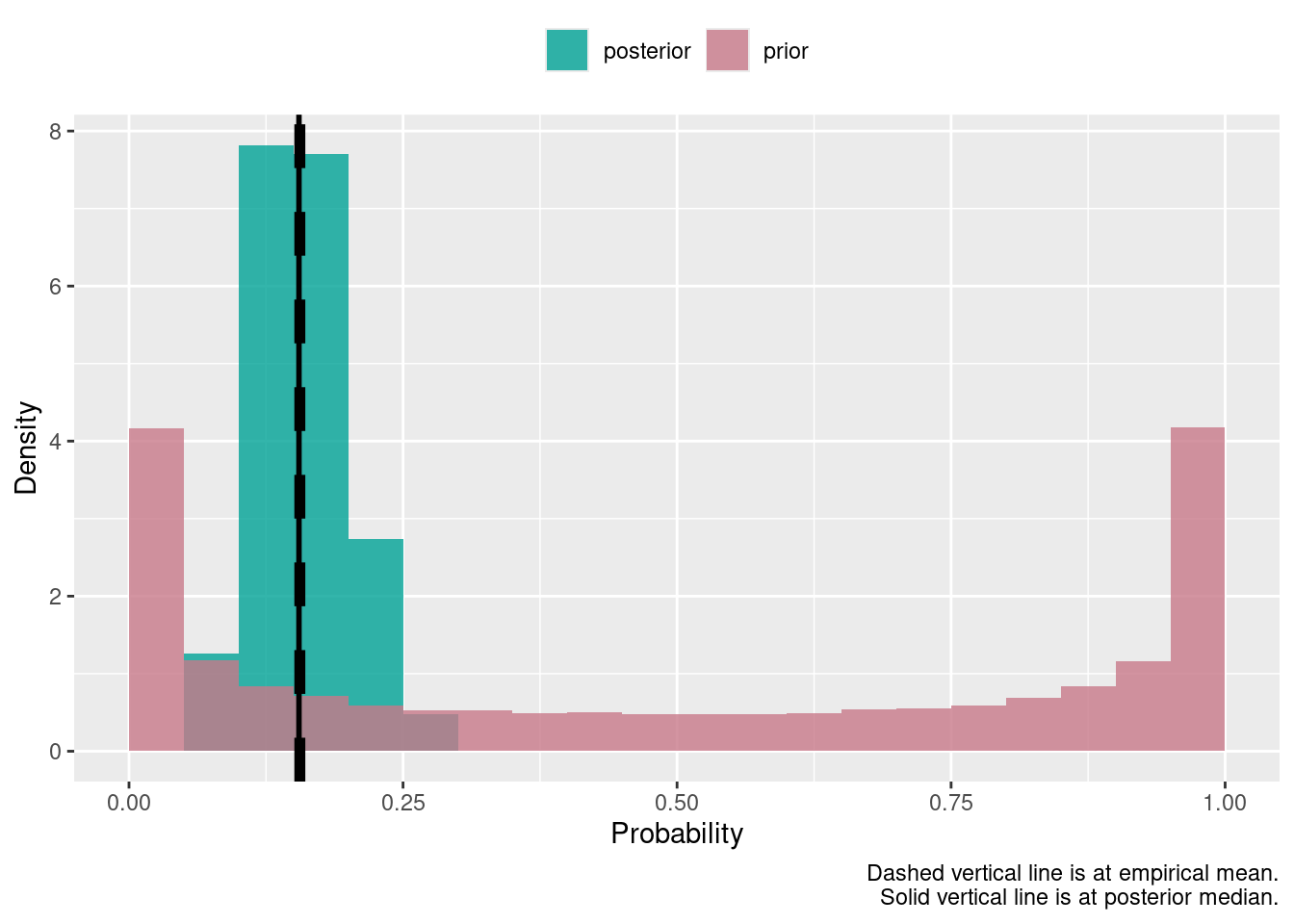

3.4.2 Example 2

This example implements a very primitive component-wise ‘L[2]-loss descent’ boosting (comparable to what add-on package mboost implements for a normally distributed response).

set.seed(123)
x1 <- drought$elev - mean(drought$elev)
x2 <- runif(nrow(drought), min = min(x1), max = max(x1))
x2 <- x2 - mean(x2)
y <- drought$bair
f_y_work <- function(y, x1, x2, b0, b1, b2){-1 * (-2*y + 2*(b0 + b1*x1 + b2*x2))}
b0 <- 0
b1 <- 0
b2 <- 0
crit_diff <- 1 ## initialize such that condition is true at beginning
crit_old <- sqrt(mean(c(y - (b0 + b1*x1 + b2*x2))^2))
component <- NULL
while (crit_diff > 0.0001) {
  y_work <- f_y_work(y = y, x1 = x1, x2 = x2, 
                     b0 = b0[length(b0)], b1 = b1[length(b1)], 
                     b2 = b2[length(b2)])
  lm_b0 <- lm(y_work ~ 1)
  lm_b1 <- lm(y_work ~ -1 + x1)
  lm_b2 <- lm(y_work ~ -1 + x2)
  crit_b0 <- mean(lm_b0$residuals^2)
  crit_b1 <- mean(lm_b1$residuals^2)
  crit_b2 <- mean(lm_b2$residuals^2)
  selected <- which.min(c(crit_b0, crit_b1, crit_b2))
  update_weight <- rep(0, 3)
  update_weight[selected] <- .01
  b0 <- c(b0, b0[length(b0)] + update_weight[1] * coef(lm_b0))
  b1 <- c(b1, b1[length(b1)] + update_weight[2] * coef(lm_b1))
  b2 <- c(b2, b2[length(b2)] + update_weight[3] * coef(lm_b2))
  component <- c(component, selected)
  crit_new <- sqrt(mean(c(y - (b0[length(b0)] + 
                                 b1[length(b1)] * x1 + 
                                 b2[length(b2)] * x2))^2))
  crit_diff <- crit_old - crit_new ## Update!
  crit_old <- crit_new
}
table(component)
## component
##   1   2   3 
## 155  81  10
paint <- colorspace::divergingx_hcl(n = length(b0), pal = "Zissou")
paint_a <- colorspace::divergingx_hcl(n = length(b0), pal = "Zissou", alpha = .1)
p1 <- ggplot(data = data.frame(x1 = x1, y = y)) + 
  geom_point(aes(x = x1, y = y))
p2 <- ggplot(data = data.frame(x2 = x2, y = y)) + 
  geom_point(aes(x = x2, y = y))
for (index in 1:length(b0)) {
  p1 <- p1 + geom_abline(intercept = b0[index], slope = b1[index], color = paint_a[index])
  p2 <- p2 + geom_abline(intercept = b0[index], slope = b2[index], color = paint_a[index])
}
cowplot::plot_grid(p1, p2, 
                   ggplot(data = data.frame(iteration = 1:length(component),
                                            component = as.numeric(as.factor(component)))) + 
                     geom_point(aes(x = iteration, y = component)) + 
                     scale_y_continuous(breaks = 1:3, minor_breaks = NULL), 
                   ncol = 1)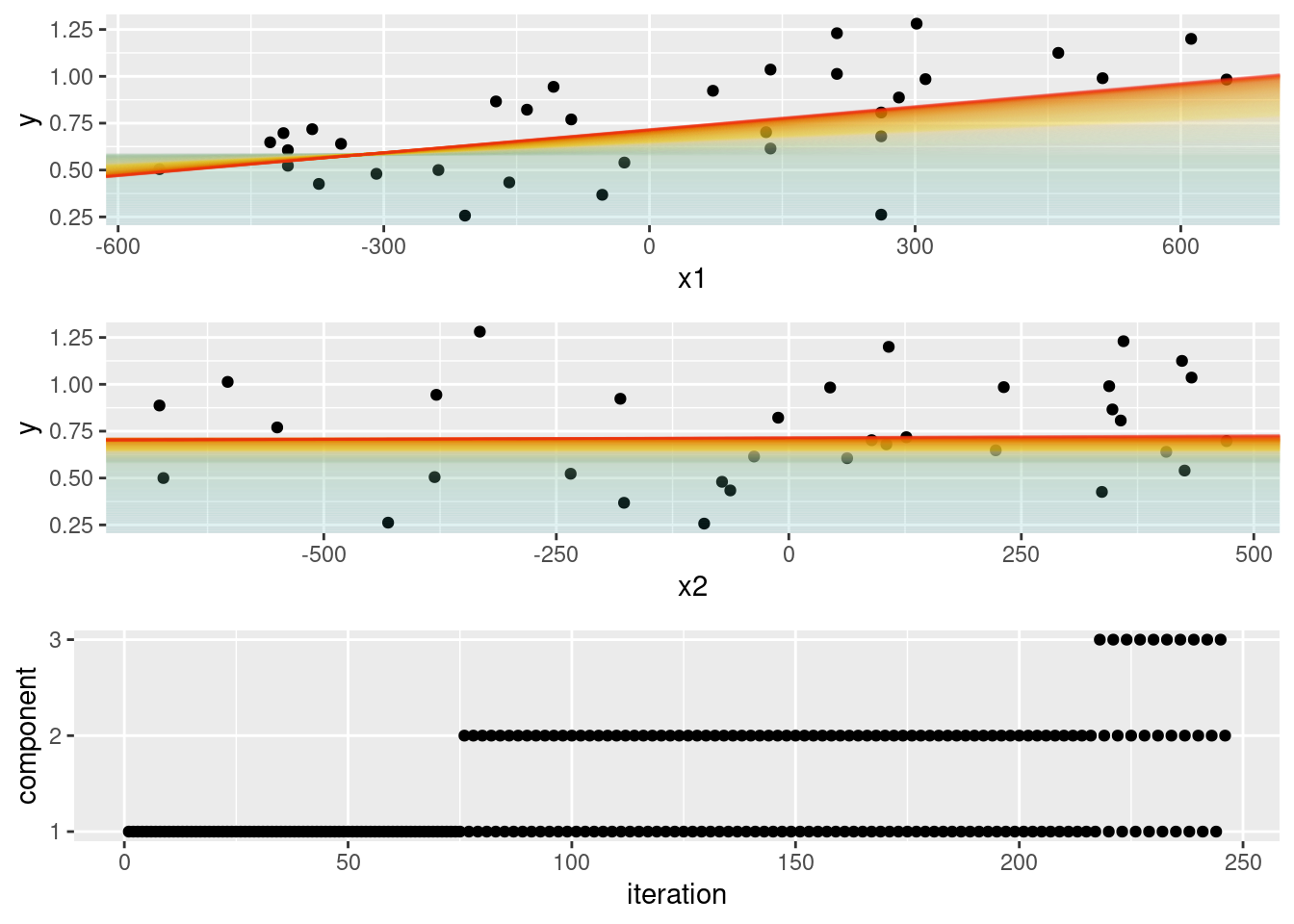

3.5 apply-commands

An apply-command applies the same function to each of the elements of a data object. This is usually done for taking the sum or calculating the arithmetic mean, or quantiles, of the columns or rows of a matrix. There are different - but actually very similar – versions of appyly.

Usage:

apply(X, MARGIN, FUN, ...) ## For matrix X: Result is a list.
lapply(X, FUN, ...) ## For list X: Result is a list.
sapply(X, FUN, ...) ## For list X: Result is a vector or another 
## Data object that the result might be 'simplified' to.
  • apply applies function (specified by FUN) to each element of the respective dimension (defined with argument MARGIN) of X.
  • MARGIN equals 1 for line-by-line, and 2 for column-wise execution.
  • ... for further arguments to FUNCTION (same for every element ofX!).
  • For lists X, MARGIN cannot be selected because lists only have one dimension.

3.5.1 Exercises

A <- matrix(ncol = 5, nrow = 10, data = 1:50)
(B <- apply(A, MARGIN = 2, FUN = mean))
class(B)
colSums(A)/nrow(A)
apply(A, MAR = 2, FUN = sd)
(B <- apply(A, MARGIN = 2, FUN = summary))
class(B)
dimnames(B)
apply(drought, MARGIN = 2, FUN = function(x){sum(is.na(x))})
apply(drought[, 1:2], MARGIN = 2, FUN = mean)
apply(drought[, 1:2], MARGIN = 1, FUN = mean)
apply(frost, MARGIN = 2, FUN = function(x){sum(is.na(x))})
apply(frost[, c(1:2, 6:7)], MARGIN = 2, FUN = mean)
lapply(frost[, c(1:2, 6:7)], FUN = mean)
sapply(frost[, c(1:2, 6:7)], FUN = mean)

3.6 plyr::ddply: ’split–apply–combine

‘split–apply–combine’ refers to a sequence of actions that is often needed for analyzing data:

  • split: Split the data set according to the characteristics of one or a combination of several categorical variables,
  • apply: Apply statistical methods (or functions like mean(), length(), …) to each of these partial data sets,
  • combine: Manage all results in a common result object.

‘split–apply–combine’ with the function ddply from the package plyr (Wickham 2011):

  • takes a dataframe (one of the ds in the functions name)
  • returns a dataframe (the second d in the functions name)

Alternative: base R aggregate.

Usage:

library("plyr")
ddply(data, 
      variables = c("variable(s) to split data frame by"), 
      summarise, 
      output_variable1 = function1(input_variable1),
      output_variable2 = function2(input_variable2),
      ...)
library("plyr")
d_breaks_cut <- quantile(df$d, probs = seq(0, 1, by = 0.05))
df$d_cut <- cut(df$d, breaks = d_breaks_cut, include.lowest = T)
dd <- ddply(df, c("d_cut"), summarise, 
            n = length(h),
            h_min = min(h),
            h_q25 = quantile(h, probs = 0.25),
            h_mean = mean(h),
            h_q75 = quantile(h, probs = 0.75),
            h_max = max(h))
head(dd)
##       d_cut  n h_min h_q25   h_mean h_q75 h_max
## 1 [1.5,3.1] 86   1.9 2.900 3.389535 3.800   6.8
## 2   (3.1,4] 91   2.1 3.600 4.410989 5.050   7.5
## 3   (4,4.8] 86   3.2 4.200 4.995349 5.800   7.9
## 4 (4.8,5.4] 79   3.1 4.550 5.401266 6.050  10.1
## 5 (5.4,6.2] 93   3.4 5.200 6.311828 7.100  15.5
## 6 (6.2,6.9] 74   3.8 5.125 6.532432 7.775   9.8

3.7 Pragmatic Programming.

The primary aim of your R Code is that it does what you need it to do – without errors!

Faulty conclusions in your data analysis as a consequence of data handling errors are one of the worst things that can happen to you as a researcher.

Copy-paste sequences such as:

df[, 1] <- df[, 1] - mean(df[, 1]) / sd(df[, 1])
df[, 2] <- df[, 2] - mean(df[, 2]) / sd(df[, 2])
df[, 3] <- df[, 3] - mean(df[, 3]) / sd(df[, 3])
df[, 5] <- df[, 5] - mean(df[, 5]) / sd(df[, 1])
df[, 6] <- df[, 6] - mean(df[, 6]) / sd(df[, 6])

are one of the main error source for R users / ‘beginners’ that don’t rely on ‘programming techniques’.

Loops are somehow ill-reputed, but whatever way of programming you find that get’s you towards errorless handling of your data, is perfect!

Therefore:

  • Use loops as often as possible (‘upwards’: wherever you can replace long copy-paste chains with an errorless loop), but avoid loops as often as necessary (‘downwards’), because – very roughly said – loops read and write to the main memory in each iteration \(\rightarrow\) Vectorized programming reads and writes only once: many functions take vectors as arguments and are therefore (often) faster.
  • Use an apply command if you want the function to do the same on every element.
  • But: Loops are simple and pragmatic and whoever masters them is already a king: It is better if R-Code gets something done slowly, but correct, than quickly, but wrong!
  • Loops cannot be avoided in an iterative processes – but this is something you will rarely need!

4 Define your own functions.

Why should I be able to define my own functions?

  • Functions generalize command sequences and make it easier and easier to try something out under many different argument values / dates / ….
  • Functions keep the workspace clean (see next section on environments).
  • Functions facilitate the reproducibility of analyzes.
  • Functions make it easier for other users to access your work.
  • As can be seen from the apply() examples, it is very often necessary to be able to write your own little helper functions. Also for your own orientation: Always comment on the processes and steps in your code and in your functions to make it easier to understand the motivation and ideas behind it later.
name <- function(arg1, arg2, arg3 = TRUE, arg4 = 2, ...){
  content
  return(result)
}
  • The general rules for naming objects also apply to function arguments.
  • Arguments can have preset values (here arg3 andarg4)
  • The last argument ... (optional) is a special argument and can be used to pass unspecified arguments to function calls.
  • Arguments changed by content and objects created are in their own local environment.
  • The result is returned to the global environment with return(result).

4.1 Naming conventions for arguments.

Argument name Inhalt
data Dataframe
x, y, z Vectors (most often with numerical elements)
n Sample size
formula Formula object
… …
  • Use function and argument names that are based on existing R functions.
  • Make arguments as self-explanatory as possible by name.

4.2 content and result.

The content block:

  • Should make it possible to carry out many similar – but different – calculations and therefore define as few objects as possible to ‘fixed values’: alternatively, always try to define arguments with default values.
  • Falls back on the higher-level environment (or environments, if necessary) if it cannot find an object in the local environment (this is known as scoping).

The result object:

  • Can be of any possible R object class (vector, list, data set, function (a function that itself returns a function is called closure), …).
  • Is generated by calling the function and stored in the global environment.
  • All other objects are no longer ‘visible’ from the global environment.

4.3 Exercises

4.3.1 Environments and scoping

rm(list = ls())
ls()
f <- function(x){
  y <- 2
  print(ls())
  y <- y + z ## f will search for z in the parent (global, here) environment.
  print(ls())
  return(x + y)
}
x <- 1; z <- 3
f(x = x) ## f will find z:
## -> although we don't explicitly use it as an argument in the local environment
##    passed to f.
y ## We cannot fall back on y from the higher-level environment.
## Error in eval(expr, envir, enclos): Objekt 'y' nicht gefunden

4.3.2 Closure

power <- function(exponent){
  return(function(x){
    return(x ^ exponent)})
}
square <- power(2)
square(2)
square(4)
cube <- power(3)
cube(2)
cube(4)

4.4 Real-world helpers

4.4.1 drop_ghosts

This function drops ghosts, ie. it removes levels of a factor variable for which the absolute frequency in the data is \(0\).

drop_ghosts <- function(x, lev = NULL) {
  if (is.null(lev)) {
    as.factor(as.character(x))  
  } else {
    if (length(unique(x)) != length(lev)) {
      stop("Please provide levels of correct length!")  
    }
    factor(as.character(x), levels = lev)
  }
}

Validation:

tmp <- data.frame(species = factor(rep(c("Beech", "Spruce"), each = 5)))
tmp$species
##  [1] Beech  Beech  Beech  Beech  Beech  Spruce Spruce Spruce Spruce Spruce
## Levels: Beech Spruce
sub <- subset(tmp, species == "Beech")
sub$species
## [1] Beech Beech Beech Beech Beech
## Levels: Beech Spruce
drop_ghosts(x = sub$species)
## [1] Beech Beech Beech Beech Beech
## Levels: Beech
drop_ghosts(x = sub$species, lev = c("Beech", "Oak"))
## Error in drop_ghosts(x = sub$species, lev = c("Beech", "Oak")): Please provide levels of correct length!
(tmp <- factor(c("Beech", "Oak"), levels = c("Beech", "Oak", "Spruce")))
## [1] Beech Oak  
## Levels: Beech Oak Spruce
drop_ghosts(x = tmp, lev = c("Beech", "Oak"))
## [1] Beech Oak  
## Levels: Beech Oak
drop_ghosts(x = tmp, lev = c("Oak", "Beech"))
## [1] Beech Oak  
## Levels: Oak Beech

4.4.2 overlap_seq

This function generates an overlapping sequence, ie. it takes a numeric variable x and a numeric step-length delta and calculates a sequence at multiples of delta that has a minimum below or just at the minumum of x, and a maximum beyond or just at the maximum of x.

overlap_seq <- function(x, delta) {
  tmp <- x %/% delta
  tmp2 <- x %% delta
  if (tmp2[which.max(x)] == 0) {
    result <- delta * (min(tmp, na.rm = T):max(tmp, na.rm = T))
  } else {
    result <- delta * (min(tmp, na.rm = T):(max(tmp, na.rm = T) + 1))
  }
  return(result)
}

Validation:

overlap_seq(c(50, 120, 290), delta = 100)
## [1]   0 100 200 300
overlap_seq(c(50, 120, 300), delta = 100)
## [1]   0 100 200 300
overlap_seq(c(0, 120, 300), delta = 100)
## [1]   0 100 200 300
overlap_seq(c(-1, 120, 301), delta = 100)
## [1] -100    0  100  200  300  400

References

Wickham, Hadley. 2011. “The Split-Apply-Combine Strategy for Data Analysis.” Journal of Statistical Software 40 (1): 1–29. http://www.jstatsoft.org/v40/i01/.

  1. Private webpage: uncertaintree.github.io↩︎